1970 Canadian MO Problems/Problem 7
Problem
Show that from any five integers, not necessarily distinct, one can always choose three of these integers whose sum is divisible by ![]() .
.
Solution
Claim 1: if ![]() ,
, ![]() , and
, and ![]() have equal modularity, then
have equal modularity, then ![]() is divisible by
is divisible by ![]()
Proof of Claim 1: Let ![]() ,
, ![]() , and
, and ![]() be three integers with equal modularity.
be three integers with equal modularity.
That is, ![]() , where
, where ![]() or
or ![]() .
.
Then ![]()
Thus, if ![]() ,
, ![]() , and
, and ![]() have equal modularity, then
have equal modularity, then ![]() is divisible by
is divisible by ![]()
Claim 2: if ![]() ,
, ![]() , and
, and ![]() have different modularity from each other, then
have different modularity from each other, then ![]() is divisible by
is divisible by ![]()
Proof of Claim 2: Let ![]() ,
, ![]() , and
, and ![]() be three integers where one of them is is divisible by 3, the other one has a reminder of 1 when divided by 3 and the other one a reminder of 2, (or -1) for simplicity.
be three integers where one of them is is divisible by 3, the other one has a reminder of 1 when divided by 3 and the other one a reminder of 2, (or -1) for simplicity.
Then ![]()
Thus, if ![]() ,
, ![]() , and
, and ![]() have different modularity from each other, then
have different modularity from each other, then ![]() is divisible by
is divisible by ![]()
In order for the sum of three integers to be divisible by three these three integers should have either all with the same modularity to each other, or they must have distinct modularity.
To have 4 integers that their sum is not divisible by three, then we can't have any combinations of 3 out of 4 where each of those are either the same modularity or different modularity with each other.
Therefore, one can chose 2 integers with the same modularity with each other and another integer with a different modularity but the same modularity with each other.
So, from integers ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , the only combinations of the modularities that we can have with 4 numbers such that no three of those numbers get a sum that divisible by three are:
, the only combinations of the modularities that we can have with 4 numbers such that no three of those numbers get a sum that divisible by three are:
Combination 1: ![]() , Combination 2:
, Combination 2: ![]() , or Combination 3:
, or Combination 3: ![]()
The fifth number ![]() will be of modularity
will be of modularity ![]() or
or ![]() .
.
Case 1: ![]()
From Combination 1, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
From Combination 2, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
From Combination 3, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
Case 2: ![]()
From Combination 1, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
From Combination 2, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
From Combination 3, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
Case 3: ![]()
From Combination 1, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
From Combination 2, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
From Combination 3, we have ![]() from which we can chose
from which we can chose ![]() which is divisible by three
which is divisible by three
And this proves that from any five integers, not necessarily distinct, one can always choose three of these integers whose sum is divisible by ![]()
~Tomas Diaz. orders@tomasdiaz.com
Solution 2
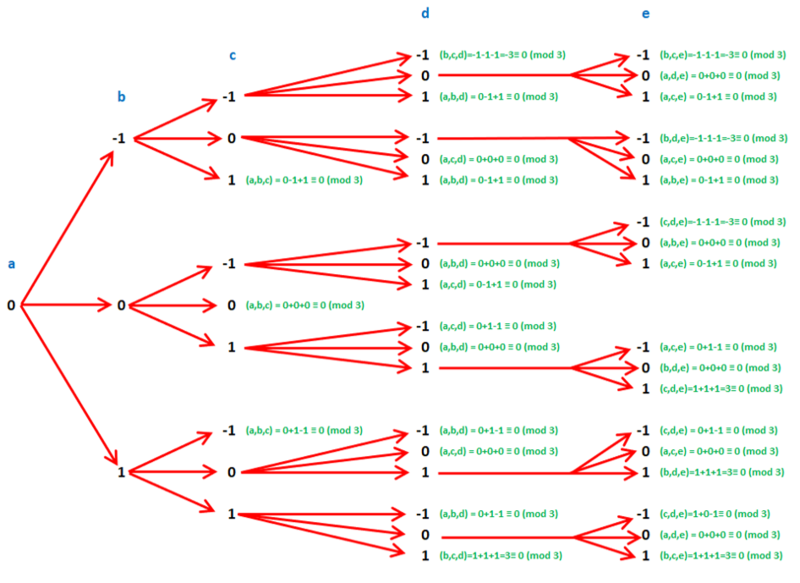
Drawing a graph tree with nodes with all the modular possibilities and their paths chowing each path how it ends when a specific combination of three out of available numbers on that path, their summation is divisible by 3:
~Tomas Diaz. orders@tomasdiaz.com
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.