1971 Canadian MO Problems
Contents
[hide]Problem 1
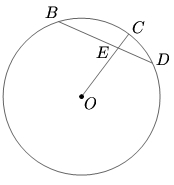
![]() is a chord of a circle such that
is a chord of a circle such that ![]() and
and ![]() Let
Let ![]() be the center of the circle. Join
be the center of the circle. Join ![]() and extend
and extend ![]() to cut the circle at
to cut the circle at ![]() Given
Given ![]() find the radius of the circle
find the radius of the circle
Problem 2
Let ![]() and
and ![]() be positive real numbers such that
be positive real numbers such that ![]() . Show that
. Show that ![]() .
.
Problem 3
![]() is a quadrilateral with
is a quadrilateral with ![]() . If
. If ![]() is greater than
is greater than ![]() , prove that
, prove that ![]() .
.
Problem 4
Determine all real numbers ![]() such that the two polynomials
such that the two polynomials ![]() and
and ![]() have at least one root in common.
have at least one root in common.
Problem 5
Let ![]() , where the coefficients
, where the coefficients ![]() are integers. If
are integers. If ![]() and
and ![]() are both odd, show that
are both odd, show that ![]() has no integral roots.
has no integral roots.
Problem 6
Show that, for all integers ![]() ,
, ![]() is not a multiple of 121.
is not a multiple of 121.
Problem 7
Let ![]() be a five digit number (whose first digit is non-zero) and let
be a five digit number (whose first digit is non-zero) and let ![]() be the four digit number formed from n by removing its middle digit. Determine all
be the four digit number formed from n by removing its middle digit. Determine all ![]() such that
such that ![]() is an integer.
is an integer.
Problem 8
A regular pentagon is inscribed in a circle of radius ![]() .
. ![]() is any point inside the pentagon. Perpendiculars are dropped from
is any point inside the pentagon. Perpendiculars are dropped from ![]() to the sides, or the sides produced, of the pentagon.
to the sides, or the sides produced, of the pentagon.
a) Prove that the sum of the lengths of these perpendiculars is constant.
b) Express this constant in terms of the radius ![]() .
.
Problem 9
Two flag poles of height ![]() and
and ![]() are situated
are situated ![]() units apart on a level surface. Find the set of all points on the surface which are so situated that the angles of elevation of the tops of the poles are equal.
units apart on a level surface. Find the set of all points on the surface which are so situated that the angles of elevation of the tops of the poles are equal.
Problem 10
Suppose that ![]() people each know exactly one piece of information, and all
people each know exactly one piece of information, and all ![]() pieces are different. Every time person
pieces are different. Every time person ![]() phones person
phones person ![]() ,
, ![]() tells
tells ![]() everything that
everything that ![]() knows, while
knows, while ![]() tells
tells ![]() nothing. What is the minimum number of phone calls between pairs of people needed for everyone to know everything? Prove your answer is a minimum.
nothing. What is the minimum number of phone calls between pairs of people needed for everyone to know everything? Prove your answer is a minimum.