1972 IMO Problems/Problem 6

Problem

Given four distinct parallel planes, prove that there exists a regular tetrahedron with a vertex on each plane.

Solution 1

Let our planes be $\pi_1,\pi_2,\pi_3,\pi_4$ , which we assume to be parallel to the $xy$ -plane, listed in the increasing order of their $z$ -coordinates. First take a plane $\pi$ orthogonal to $\pi_i$ , which cuts $\pi_1,\pi_2,\pi_3$ along three lines $d_1,d_2,d_3$ . On these three lines, take three vertices $A_1,A_2,A_3$ respectively of an equilateral triangle (it is well-known that this is possible; in fact, the problem here is the $3$ -dimensional version of this), and then complete the two regular tetrahedra $A_1A_2A_3P_1,A_1A_2A_3P_2$ having $A_1A_2A_3$ as one of their faces. Both $P_i$ lie below $\pi_4$ .

Now take another plane $\pi$ and repeat the construction above. If $\pi$ makes a small enough angle with the $\pi_i$ 's, one of the $P_i$ 's we get this time must lie above $\pi_4$ . Now, if we move the initial position of $\pi$ towards the new one continuously and record the $z$ -coordinates of $P_1,P_2$ , these will be continuous functions of the angle that $\pi$ makes with $\pi_i$ , and for one of the points $P_1,P_2$ the $z$ -coordinate will move continuously from being smaller than that of $\pi_4$ to being larger than it, meaning that at some point, one of the points $P_1,P_2$ will lie on $\pi_4$ , and this is what we want.

The above solution was posted and copyrighted by grobber. The original thread for this problem can be found here: [1]

Solution 2

Let's denote the (directed) distance between two parallel planes p and p' by d (p; p'), and the (directed) distance between two parallel lines g and g' by d (g; g'). (Directed distances are defined as follows: If $p_1$ , $p_2$ , $p_3$ , ... is a family of parallel planes in space, then we choose a unit vector $\overrightarrow{v}_p$ perpendicular to all of these planes (there are two such unit vectors, and we have to choose one of them), and then, by the directed distance between two of these planes $p_i$ and $p_j$ , we denote the real number k such that the translation with translation vector $k\cdot\overrightarrow{v}_p$ maps the plane $p_i$ to the plane $p_j$ . Similarly, we define the directed distance between two of a family of parallel lines in a plane.)

The problem can be rewritten as follows: Given four distinct parallel planes $p_1$ , $p_2$ , $p_3$ , $p_4$ in space, prove that there exists a regular tetrahedron XYZW such that $X\in p_1$ , $Y\in p_2$ , $Z\in p_3$ , $W\in p_4$ .

In order to do this, it is enough to find a regular tetrahedron ABCD somewhere in space and four parallel planes $q_1$ , $q_2$ , $q_3$ , $q_4$ such that $A\in q_1$ , $B\in q_2$ , $C\in q_3$ , $D\in q_4$ and $d\left(q_1;\;q_2\right): d\left(q_2;\;q_3\right): d\left(q_3;\;q_4\right)=d\left(p_1;\;p_2\right): d\left(p_2;\;p_3\right): d\left(p_3;\;p_4\right)$ . In fact, once we have found such a tetrahedron ABCD and such planes $q_1$ , $q_2$ , $q_3$ , $q_4$ , then, because of $p_1\parallel p_2\parallel p_3\parallel p_4$ , $q_1\parallel q_2\parallel q_3\parallel q_4$ and $d\left(q_1;\;q_2\right): d\left(q_2;\;q_3\right): d\left(q_3;\;q_4\right)=d\left(p_1;\;p_2\right): d\left(p_2;\;p_3\right): d\left(p_3;\;p_4\right)$ , there exists a similitude transformation which maps the planes $q_1$ , $q_2$ , $q_3$ , $q_4$ to the planes $p_1$ , $p_2$ , $p_3$ , $p_4$ ; this similitude transformation will then obviously map the regular tetrahedron ABCD with $A\in q_1$ , $B\in q_2$ , $C\in q_3$ , $D\in q_4$ to a regular tetrahedron XYZW with $X\in p_1$ , $Y\in p_2$ , $Z\in p_3$ , $W\in p_4$ ; hence, the existence of such a tetrahedron XYZW will be proven, and the problem will be solved.

So consider a regular tetrahedron ABCD lying arbitrarily in space; we try to find four parallel planes $q_1$ , $q_2$ , $q_3$ , $q_4$ such that $A\in q_1$ , $B\in q_2$ , $C\in q_3$ , $D\in q_4$ and $d\left(q_1;\;q_2\right): d\left(q_2;\;q_3\right): d\left(q_3;\;q_4\right)=d\left(p_1;\;p_2\right): d\left(p_2;\;p_3\right): d\left(p_3;\;p_4\right)$ .

In fact, we start working in the plane ABC. Let T be the point on the line AC such that $AT: TC=d\left(p_1;\;p_2\right): d\left(p_2;\;p_3\right)$ (where the segments AT and TC are directed). Let $g_2$ be the line BT, and let $g_1$ and $g_3$ be the parallels to the line $g_2=BT$ through the points A and C, respectively. Then, the lines $g_1$ , $g_2$ , $g_3$ are parallel and, by Thales, $d\left(g_1;\;g_2\right): d\left(g_2;\;g_3\right)=AT: TC$ . Thus, $d\left(g_1;\;g_2\right): d\left(g_2;\;g_3\right)=d\left(p_1;\;p_2\right): d\left(p_2;\;p_3\right)$ . Now, denote by $g_4$ the line in the plane ABC which is parallel to the lines $g_1$ , $g_2$ , $g_3$ and satisfies $d\left(g_1;\;g_2\right): d\left(g_2;\;g_3\right): d\left(g_3;\;g_4\right)=d\left(p_1;\;p_2\right): d\left(p_2;\;p_3\right): d\left(p_3;\;p_4\right)$ .

Now, let $q_4$ be the plane passing through the line $g_4$ and the point D. Let $q_1$ , $q_2$ , $q_3$ be the planes parallel to $q_4$ and passing through the lines $g_1$ , $g_2$ , $g_3$ , respectively (of course, we can construct such planes since the lines $g_1$ , $g_2$ , $g_3$ are parallel to $g_4$ ). Thus, we have found four parallel planes $q_1$ , $q_2$ , $q_3$ , $q_4$ such that $A\in q_1$ , $B\in q_2$ , $C\in q_3$ , $D\in q_4$ , and these planes obviously satisfy $d\left(q_1;\;q_2\right): d\left(q_2;\;q_3\right): d\left(q_3;\;q_4\right)=d\left(g_1;\;g_2\right): d\left(g_2;\;g_3\right): d\left(g_3;\;g_4\right)$ . Since $d\left(g_1;\;g_2\right): d\left(g_2;\;g_3\right): d\left(g_3;\;g_4\right)=d\left(p_1;\;p_2\right): d\left(p_2;\;p_3\right): d\left(p_3;\;p_4\right)$ , we thus have $d\left(q_1;\;q_2\right): d\left(q_2;\;q_3\right): d\left(q_3;\;q_4\right)=d\left(p_1;\;p_2\right): d\left(p_2;\;p_3\right): d\left(p_3;\;p_4\right)$ . Hence, according to the above, the problem is solved.

The above solution was posted and copyrighted by darij grinberg. The original thread for this problem can be found here: [2]

Remarks (added by pf02, May 2025)

1. The first "solution" is based on a good idea, but it is so incomplete (it contains so mach hand-waiving) that it can not be called a solution. Here are the issues with this "solution":

a. The first problem (minor) is the statement "On these three lines, take three vertices $A_1, A_2, A_3$ respectively of an equilateral triangle (it is well-known that this is possible...)". This is *not* well known, it should be proven.

b. The second problem (a more serious one) is the statement that "If $\pi$ makes a small enough angle with the $\pi_i$ 's, one of the $P_i$ 's we get this time must lie above $\pi_4$ ". This is probably true, but not obvious at all, and it should have a proof.

c. The third problem (this is so serious that it is a "show stopper") is the assumption (not stated explicitly) that the $z$ -coordinates of $P_1, P_2$ as functions of the angle $\theta$ between $\pi$ and $\pi_i$ are continuous functions. This is not even true as stated, it depends on the choice of $A_1, A_2, A_3$ .

As I said, the idea is good, and this could be turned into a solution to the problem. I leave this task to the diligent reader.

2. Below, I will give another solution to the problem. It is similar to solution 2, but different enough to warrant writing it down. Both this solution, and solution 2, show that in fact, the tetrahedron does not have to be regular. The problem could be restated as "Given four distinct parallel planes and a tetrahedron, prove that there exists a tetrahedron similar to the given one with a vertex on each plane."

Solution 3

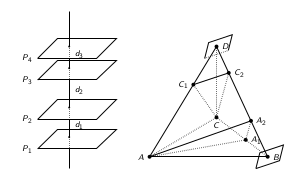
As I remarked, this solution is similar with the previous one. Let $P_1, P_2, P_3, P_4$ be the four planes. We can assume they are horizontal (in some $x, y, z$ coordinate system in which the $z$ axis is vertical) and that their $z$ coordinates are in increasing order. Let $d_1$ be the distance between $P_1, P_2$ , $d_2$ be the distance between $P_2, P_3$ , and $d_3$ be the distance between $P_3, P_4$ .

Now consider the tetrahedron $ABCD$ . Take $C_1 \in AD, A_1 \in BC$ and $C_2, A_2 \in BD$ such that

$\frac{DC_1}{C_1A} = \frac{d_3}{d_2} \hspace{52pt} (1)$

$\frac{CA_1}{A_1B} = \frac{d_2}{d_1} \hspace{52pt} (2)$

$\frac{DC_2}{C_2B} = \frac{d_3}{d_2 + d_1} \hspace{30pt} (3)$

$\frac{DA_2}{A_2B} = \frac{d_3 + d_2}{d_1} \hspace{30pt} (4)$ .

Note that (3) and (4) imply

$\frac{DC_2}{C_2A_2} = \frac{d_3}{d_2} \hspace{52pt} (5)$

$\frac{C_2A_2}{A_2B} = \frac{d_2}{d_1} \hspace{52pt} (6)$ .

(1) and (5) imply that $C_1C_2 \parallel AA_2$ . Also, (2) and (6) imply that $CC_2 \parallel A_1A_2$ . From these it follows that the planes $(CC_1C_2)$ and $(AA_1A_2)$ are parallel.

Now take two planes $P_B$ through $B$ , and $P_D$ through $D$ parallel to the parallel planes $(CC_1C_2)$ and $(AA_1A_2)$ . If we denote $e_1, e_2, e_3$ the distances between $P_B$ and $(AA_aA_2)$ , the plane $(AA_aA_2)$ and $(CC_1C_2)$ , and finally, $(CC_1C_2)$ and $P_D$ , then (5) and (6) imply that

$\frac{d_1}{d_2} = \frac{e_1}{e_2}$ and $\frac{d_2}{d_3} = \frac{e_2}{e_3} \hspace{50pt} (7)$ .

From this it follows that we can find a similar transformation in the 3D space which takes our four planes into the four planes $P_1, P_2, P_3, P_4$ . To make this explicit, we first take a rotation followed by a translation which takes $P_B$ into $P_1$ . Now we take a scaling (with suitable origin and factor) which keeps $P_1$ in place, and maps the image of $(AA_1A_2)$ obtained so far into $P_2$ . Because of (7), the image of $(CC_1C_2)$ will map into $P_3$ and the image of $P_D$ will map into $P_4$ .

Through these transformations, the image of the tetrahedron $ABCD$ will map into a similar tetrahedron with its vertices on $P_1, P_2, P_3, P_4$ .

[Solution by pf02, May 2025]

1972 IMO (Problems) • Resources
Preceded by Problem 5	1 • 2 • 3 • 4 • 5 • 6	Followed by Last Question
All IMO Problems and Solutions

Page

Toolbox

Search