1978 IMO Problems/Problem 2
Problem
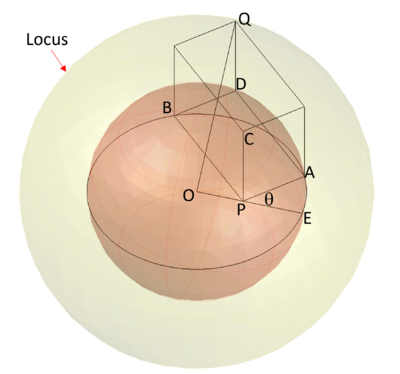
We consider a fixed point ![]() in the interior of a fixed sphere
in the interior of a fixed sphere![]() We construct three segments
We construct three segments ![]() , perpendicular two by two
, perpendicular two by two![]() with the vertexes
with the vertexes ![]() on the sphere
on the sphere![]() We consider the vertex
We consider the vertex ![]() which is opposite to
which is opposite to ![]() in the parallelepiped (with right angles) with
in the parallelepiped (with right angles) with ![]() as edges
as edges![]() Find the locus of the point
Find the locus of the point ![]() when
when ![]() take all the positions compatible with our problem.
take all the positions compatible with our problem.
Solution
Let ![]() be the radius of the given fixed sphere.
be the radius of the given fixed sphere.
Let point ![]() be the center of the sphere.
be the center of the sphere.
Let point ![]() be the 4th vertex of the face of the parallelepiped that contains points
be the 4th vertex of the face of the parallelepiped that contains points ![]() ,
, ![]() , and
, and ![]() .
.
Let point ![]() be the point where the line that passes through
be the point where the line that passes through ![]() intersects the circle on the side nearest to point
intersects the circle on the side nearest to point ![]()
Let ![]()
We start the calculations as follows:
![]()
![]()
Therefore, ![]() [Equation 1]
[Equation 1]
Using law of cosines:
![]()
![]()
![]()
![]() [Equation 2]
[Equation 2]
Using law of cosines again we also get:
![]()
Since ![]() , then
, then
![]()
![]() [Equation 3]
[Equation 3]
Substituting [Equation 2] and [Equation 3] into [Equation 1] we get:
![]() [Equation 4]
[Equation 4]
Now we apply the law of cosines again:
![]()
![]()
![]()
![]()
![]()
Since, ![]() and
and ![]() then,
then,
![]()
![]() [Equation 5]
[Equation 5]
Substituting [Equation 4] into [Equation 5] we get:
![]()
Notice that all of the terms with ![]() cancel and thus we're left with:
cancel and thus we're left with:
![]() regardless of
regardless of ![]() . [Equation 6]
. [Equation 6]
Now we need to find ![]()
Since points ![]() ,
, ![]() , and
, and ![]() are on the plane perpendicular to the plane with points
are on the plane perpendicular to the plane with points ![]() ,
, ![]() , and
, and ![]() , then these points lie on the big circle of the sphere. Therefore the distance
, then these points lie on the big circle of the sphere. Therefore the distance ![]() can be found using the formula:
can be found using the formula:
![]()
Solving for ![]() we get:
we get:
![]() [Equation 7]
[Equation 7]
Now we need to get ![]() which will be using the formula:
which will be using the formula:
![]() [Equation 8]
[Equation 8]
Substituting [Equation 6] and [Equation 7] into [Equation 8] we get:
![]()
This results in:
![]()
which is constant regardless of ![]() and constant regardless of where points
and constant regardless of where points ![]() ,
, ![]() , and
, and ![]() are located as long as they're still perpendicular to each other.
are located as long as they're still perpendicular to each other.
In space, this is a sphere with radius ![]() which is equal to
which is equal to ![]()
Therefore, the locus of vertex ![]() is a sphere of radius
is a sphere of radius ![]() with center at
with center at ![]() , where
, where ![]() is the radius of the given sphere and
is the radius of the given sphere and ![]() the distance from the center of the given sphere to point
the distance from the center of the given sphere to point ![]()
~ Tomas Diaz. orders@tomasdiaz.com
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See Also
| 1978 IMO (Problems) • Resources | ||
| Preceded by Problem 1 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 3 |
| All IMO Problems and Solutions | ||