1979 USAMO Problems/Problem 2
Problem
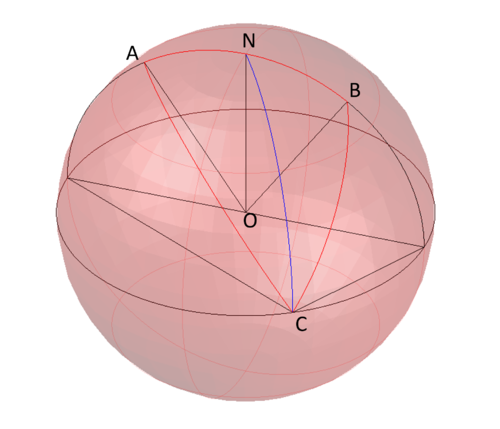
![]() is the north pole.
is the north pole. ![]() and
and ![]() are points on a great circle through
are points on a great circle through ![]() equidistant from
equidistant from ![]() .
. ![]() is a point on the equator. Show that the great circle through
is a point on the equator. Show that the great circle through ![]() and
and ![]() bisects the angle
bisects the angle ![]() in the spherical triangle
in the spherical triangle ![]() (a spherical triangle has great circle arcs as sides).
(a spherical triangle has great circle arcs as sides).
Solution
Since ![]() is the north pole, we define the Earth with a sphere of radius one in space with
is the north pole, we define the Earth with a sphere of radius one in space with ![]() and sphere center
and sphere center ![]() We then pick point
We then pick point ![]() on the sphere and define the
on the sphere and define the ![]() -plane as the plane that contains great circle points
-plane as the plane that contains great circle points ![]() ,
, ![]() , and
, and ![]() with the
with the ![]() -axis perpendicular to the
-axis perpendicular to the ![]() -axis and in the direction of
-axis and in the direction of ![]() .
.
Using this coordinate system and ![]() ,
, ![]() , and
, and ![]() axes
axes ![]() where
where ![]() is the angle from the
is the angle from the ![]() -plane to
-plane to ![]() or latitude on this sphere with
or latitude on this sphere with ![]()
Since ![]() and
and ![]() are points on a great circle through
are points on a great circle through ![]() equidistant from
equidistant from ![]() , then
, then ![]()
Since ![]() is a point on the equator, then
is a point on the equator, then ![]() where
where ![]() is the angle on the
is the angle on the ![]() -plane from the origin to
-plane from the origin to ![]() or longitude on this sphere with
or longitude on this sphere with ![]()
We note that vectors from the origin to points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are all unit vectors because all those points are on the unit sphere.
are all unit vectors because all those points are on the unit sphere.
So, we're going to define points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() as unit vectors with their coordinates.
as unit vectors with their coordinates.
We also define the following vectors as follows:
Vector ![]() is the unit vector in the direction of arc
is the unit vector in the direction of arc ![]() and tangent to the great circle of
and tangent to the great circle of ![]() at
at ![]()
Vector ![]() is the unit vector in the direction of arc
is the unit vector in the direction of arc ![]() and tangent to the great circle of
and tangent to the great circle of ![]() at
at ![]()
Vector ![]() is the unit vector in the direction of arc
is the unit vector in the direction of arc ![]() and tangent to the great circle of
and tangent to the great circle of ![]() at
at ![]()
To calculate each of these vectors we shall use the cross product as follows:
![]()
![]()
![]()
![]()
![]()
Vector ![]() :
:
![]()
![]()
![]()
Since we're only interested in the ![]() component of the vector
component of the vector
![]()
![]()
Vector ![]() :
:
![]()
![]()
![]()
Since we're only interested in the ![]() component of the vector
component of the vector
![]()
![]()
Since we're working with unit vectors, then we can use dot products on the vectors with their angles as follows:
![]()
![]()
Likewise,
![]()
![]()
Therefore,
![]() and thus
and thus ![]()
Since those angles are equal, it proves that the great circle through ![]() and
and ![]() bisects the
bisects the ![]() in the spherical triangle
in the spherical triangle ![]()
~Tomas Diaz. orders@tomasdiaz.com
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
See Also
| 1979 USAMO (Problems • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 | ||
| All USAMO Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()