1988 AIME Problems/Problem 7
Problem
In triangle ![]() ,
, ![]() , and the altitude from
, and the altitude from ![]() divides
divides ![]() into segments of length 3 and 17. What is the area of triangle
into segments of length 3 and 17. What is the area of triangle ![]() ?
?
Solution
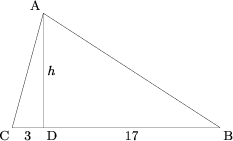
Call ![]()
![]() and
and ![]()
![]() . So,
. So, ![]() and
and ![]() . Using the tangent addition formula
. Using the tangent addition formula ![]() , we get
, we get  .
.
Simplifying, we get ![]() . Cross-multiplying and simplifying, we get
. Cross-multiplying and simplifying, we get ![]() . Factoring, we get
. Factoring, we get ![]() , so we take the positive positive solution, which is
, so we take the positive positive solution, which is ![]() . Therefore, the answer is
. Therefore, the answer is ![]() , so the answer is
, so the answer is ![]() .
.
~Arcticturn
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









