1991 OIM Problems/Problem 1
Problem
Each vertex of a cube is assigned the value of +1 or -1, and each face is assigned the product of the values assigned to each vertex. What values can the sum of the 14 numbers thus obtained take?
~translated into English by Tomas Diaz. ~orders@tomasdiaz.com
Solution
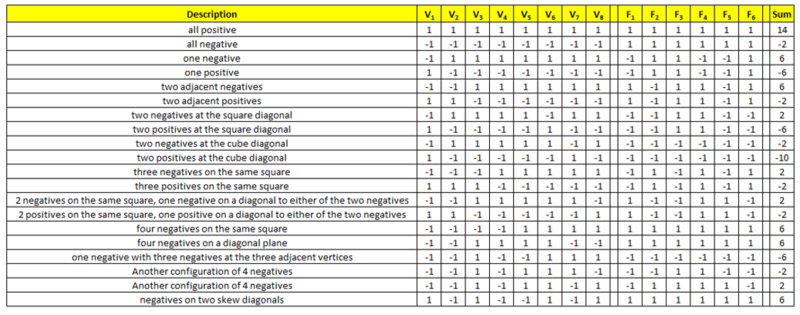
I don't have any other better method than to try all configurations:
In the table, 
is vertex 
and 
is face 
. I added all of the numbers in the rows. Granted, with spreadsheet software is easier than pen and paper, but it is still doable with it.
From the table the possible values of the sum are: -10, -6, -2, 2, 6, and 14
- Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I got partial points because I probably missed one or two of the cases when I tried all of the possible cases. At the competition I drew all the combinations. There's probably a much better method for this than trying out all the cases in this fashion. Please add such solution. I also verified all the solution to this problem with a computer code just in case. Some solutions out there include -14 and 10 as possible solutions But all of the possible 256 combinations of +1 and -1 on the vertices none of the sums in the computer came out at either of those numbers. It is possible that the key wrongfully included those wrong answers at the competition.
~Tomas Diaz. orders@tomasdiaz.com
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.
