1991 OIM Problems/Problem 2

Problem

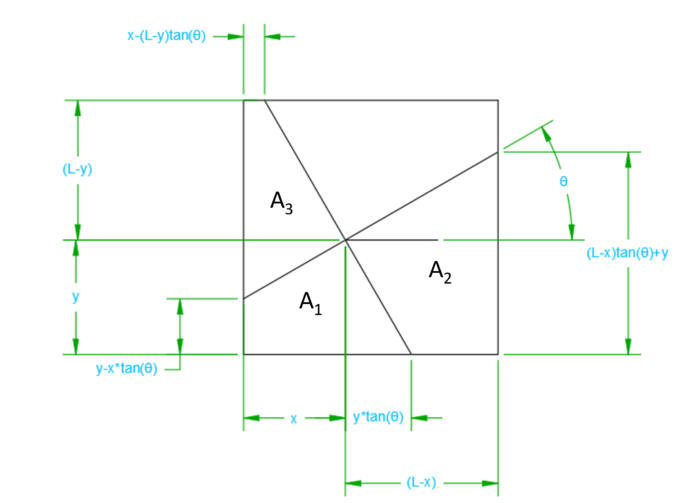
Two perpendicular lines divide a square into four parts, three of which each have an area equal to 1. Show that the area of the square is four.

~translated into English by Tomas Diaz. ~orders@tomasdiaz.com

Solution

First let's find the area of $A_1$ :

$A_1=x\frac{y-x.tan(\theta)+y}{2}+\frac{y^2tan(\theta)}{2}$

$A_1=\frac{y^2-x^2}{2}tan(\theta)+xy=1$

Now lets find the area of $A_2$ :

$A_2=\frac{L-x}{2}((L-x)tan(\theta)+y+y)-\frac{y^2}{2}tan(\theta)$

$A_2=\frac{(L-x)^2-y^2}{2}tan(\theta)+(L-x)y=1$

Now lets find the area of $A_3$ :

$A_3=\frac{L-y}{2}(x+x-(L-y)tan(\theta))+\frac{x^2}{2}tan(\theta)$

$A_3=\frac{x^2-(L-y)^2}{2}tan(\theta)+x(L-y)=1$

Now we need to solve for $x$ , $y$ and $L$ in the following system of equations:

$\begin{cases} \frac{y^2-x^2}{2}tan(\theta)+xy=1\\ \frac{(L-x)^2-y^2}{2}tan(\theta)+(L-x)y=1\\ \frac{x^2-(L-y)^2}{2}tan(\theta)+x(L-y)=1 \end{cases}$

We need the solution to be independent of $tan(\theta)$ , so the coefficient in front of that in all three equations need to be zero. Starting with the first equation we can find that condition and see if the conditions holds in the other two equations. Therefore,

$\frac{y^2-x^2}{2}=0$ which means that $x=y$

Thus,

$\frac{y^2-x^2}{2}tan(\theta)+xy=xy=1$ and since $x=y$ , then $x=y=1$

We substitute in the next two equations:

$\begin{cases} \frac{(L-1)^2-1^2}{2}tan(\theta)+(L-1)=1\\ \frac{1^2-(L-1)^2}{2}tan(\theta)+(L-1)=1 \end{cases}$

and realize that the coefficients for $tan(\theta)$ cancel to zero when $L=2$ which turns each equation into $(L-1)=1$ which verifies that $L=2$ and providing the positive solution for the system of equations as $x=y=1$ , $L=2$ , independent of $\theta$ as long as the lines go from one side to the opposite side and not to the adjacent side in each case.

Therefore, since $L=2$ , then the area of the square is $L^2=4$

This is not the most elegant solution and if I would have submitted this in the competition I would have most likely not goten full points. If you have a better solution, please add it.

Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. I got partial points because I couldn't prove this but had somewhat of an approach to get there.

~Tomas Diaz. orders@tomasdiaz.com

Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.

Page

Toolbox

Search

1991 OIM Problems/Problem 2

Problem

Solution

See also