1991 OIM Problems/Problem 6
Problem
Given 3 non-aligned points ![]() ,
, ![]() and
and ![]() , we know that
, we know that ![]() and
and ![]() are midpoints of two sides of a triangle and that
are midpoints of two sides of a triangle and that ![]() is the point of intersection of the heights of said triangle. Build the triangle.
is the point of intersection of the heights of said triangle. Build the triangle.
~translated into English by Tomas Diaz. ~orders@tomasdiaz.com
Solution
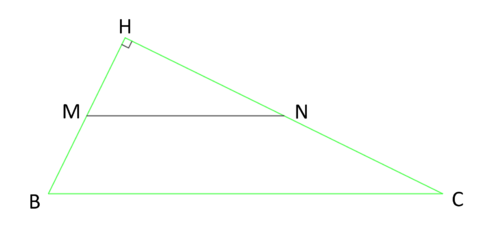
Case 1: ![]()
If you measure ![]() on the given points and it happens to be a right angle, then constructing the triangle is easy because point
on the given points and it happens to be a right angle, then constructing the triangle is easy because point ![]() is also point
is also point ![]() of the triangle
of the triangle ![]() . One can notice if this angle is a right angle or not if you can draw a perpendicular from point
. One can notice if this angle is a right angle or not if you can draw a perpendicular from point ![]() to line
to line ![]() and it passes through
and it passes through ![]() . If this happens to be the case, then since
. If this happens to be the case, then since ![]() and
and ![]() then one can simply draw a circle with the compass at points
then one can simply draw a circle with the compass at points ![]() and
and ![]() with radiuses measuring
with radiuses measuring ![]() and
and ![]() respectively. Then extend the lines
respectively. Then extend the lines ![]() and
and ![]() to the intersection on their respective circles at
to the intersection on their respective circles at ![]() and
and ![]() respectively. Then draw triangle
respectively. Then draw triangle ![]() .
.
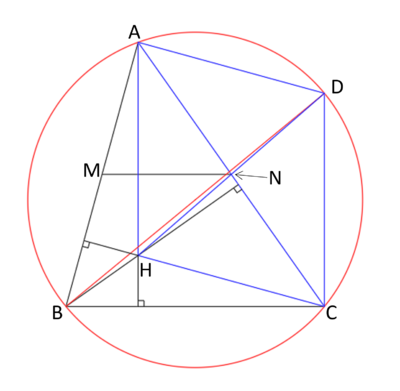
Case 2: ![]()
Let the red circle in the image above be the circumcircle of triangle ![]() . Let
. Let ![]() be a diameter of the circle. This means that
be a diameter of the circle. This means that ![]() and
and ![]() are both equal to
are both equal to ![]() because right angle triangles inscribed in circles with the hypothenuse on the diameter. Therefore
because right angle triangles inscribed in circles with the hypothenuse on the diameter. Therefore ![]() is parallel to
is parallel to ![]() and
and ![]() is parallel to
is parallel to ![]() . Thus quadrilateral
. Thus quadrilateral ![]() is a parallelogram with
is a parallelogram with ![]() in the center and
in the center and ![]() . So, one can draw point
. So, one can draw point ![]() using
using ![]() and
and ![]() . Since
. Since ![]() , then
, then ![]() is the diameter of a circle that also passes through
is the diameter of a circle that also passes through ![]() . This means that one can find point
. This means that one can find point ![]() from the intersection of this circle and the perpendicular to
from the intersection of this circle and the perpendicular to ![]() that passes through
that passes through ![]() and we can now start our construction as follows:
and we can now start our construction as follows:
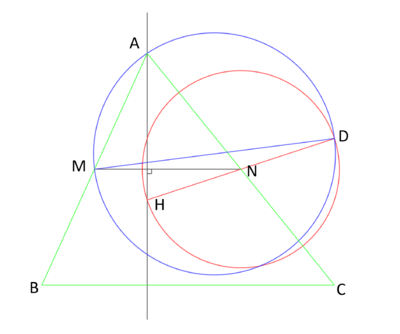
Given the points ![]() ,
, ![]() , and
, and ![]() , we first draw a perpendicular from point
, we first draw a perpendicular from point ![]() to
to ![]() with straight edge and compass using the traditional known method of finding tow points from
with straight edge and compass using the traditional known method of finding tow points from ![]() on
on ![]() equidistant to
equidistant to ![]() and from those two points drawing the perpendicular bisector to them. That way we can draw the black perpendicular line.
and from those two points drawing the perpendicular bisector to them. That way we can draw the black perpendicular line.
Then, with the compass draw the red circle with center at ![]() and radius
and radius ![]() . From
. From ![]() we extend the line
we extend the line ![]() and where it intersects the red circle that's our point
and where it intersects the red circle that's our point ![]() . We then draw blue line
. We then draw blue line ![]() and find it's bisection point using traditional bisection method with compass and straight edge. From this bisection point and the compass using that as its center we can draw the blue circle. This blue circle intersects the black perpendicular line at
and find it's bisection point using traditional bisection method with compass and straight edge. From this bisection point and the compass using that as its center we can draw the blue circle. This blue circle intersects the black perpendicular line at ![]() . Since
. Since ![]() and
and ![]() then one can simply draw a circle with the compass at points
then one can simply draw a circle with the compass at points ![]() and
and ![]() with radiuses measuring
with radiuses measuring ![]() and
and ![]() respectively. Then extend the lines
respectively. Then extend the lines ![]() and
and ![]() to the intersection on their respective circles at
to the intersection on their respective circles at ![]() and
and ![]() respectively. Then draw triangle
respectively. Then draw triangle ![]() .
.
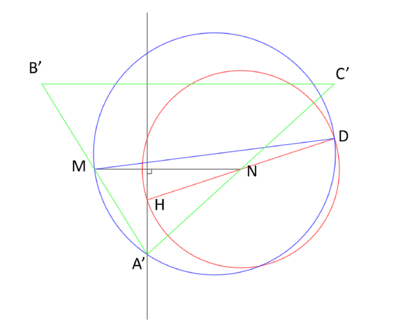
But the given points do not give us one unique triangle. It gives us two because the blue circle also intersects the black perpendicular line at another point. We will call this point ![]() . Then using the same methods as described in the procedure for triangle
. Then using the same methods as described in the procedure for triangle ![]() we find triangle
we find triangle ![]() which also has the given points
which also has the given points ![]() and
and ![]()
And this provides all of the cases and all of the triangles we can draw from those given points.
- Note. I actually competed at this event in Argentina when I was in High School representing Puerto Rico. If I remember correctly I solved the case 1 described here as it was the easiest and then wasted a lot of time trying to figure out a way unsuccessfully. I also noted that two triangles could be build instead of just one. I think they awarded me 3 points out of 10.
~Tomas Diaz. ~orders@tomasdiaz.com
Alternate solutions are always welcome. If you have a different, elegant solution to this problem, please add it to this page.