2007 AMC 12B Problems/Problem 25
Contents
[hide]Problem
Points ![]() and
and ![]() are located in 3-dimensional space with
are located in 3-dimensional space with ![]() and
and ![]() . The plane of
. The plane of ![]() is parallel to
is parallel to ![]() . What is the area of
. What is the area of ![]() ?
?
![]()
Solution 1
Link to graph: https://www.math3d.org/pHFSD6vRi
Let ![]() , and
, and ![]() . Since
. Since ![]() , we could let
, we could let ![]() ,
, ![]() , and
, and ![]() . Now to get back to
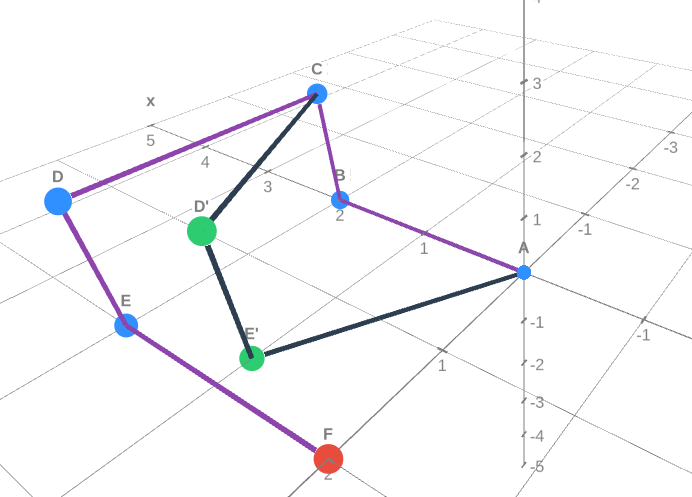
. Now to get back to ![]() we need another vertex
we need another vertex ![]() . Now if we look at this configuration as if it was two dimensions, we would see a square missing a side if we don't draw
. Now if we look at this configuration as if it was two dimensions, we would see a square missing a side if we don't draw ![]() . Now we can bend these three sides into an equilateral triangle, and the coordinates change:
. Now we can bend these three sides into an equilateral triangle, and the coordinates change: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Checking for all the requirements, they are all satisfied. Now we find the area of triangle
. Checking for all the requirements, they are all satisfied. Now we find the area of triangle ![]() . The side lengths of this triangle are
. The side lengths of this triangle are ![]() , which is an isosceles right triangle. Thus the area of it is
, which is an isosceles right triangle. Thus the area of it is ![]() .
.
Solution 2
Similar to solution 1, we allow
![]() ,
, ![]() , and
, and ![]() . This creates the isosceles right triangle on the plane of
. This creates the isosceles right triangle on the plane of ![]()
Now, note that ![]() . This means that there exists some vector
. This means that there exists some vector ![]() parallel to the plane of
parallel to the plane of ![]() that forms two right angles with
that forms two right angles with ![]() and
and ![]() . By definition, this is the cross product of the two vectors
. By definition, this is the cross product of the two vectors ![]() and
and ![]() . Finding this cross product, we take the determinant of vectors
. Finding this cross product, we take the determinant of vectors
![]() and
and
![]() *Note that z is constant because the line is parallel to the plane*
*Note that z is constant because the line is parallel to the plane*
to get ![]()
Because there can be no movement in the ![]() direction, the k unit vector must be zero. Also, because the i unit vector must be orthogonal and also 0. Thus, the vector of line
direction, the k unit vector must be zero. Also, because the i unit vector must be orthogonal and also 0. Thus, the vector of line ![]() is simply
is simply ![]()
From this, you can figure out that line ![]() , and the area of
, and the area of ![]() .
.
See also
| 2007 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()