2010 AMC 10B Problems/Problem 20
Contents
[hide]Problem
Two circles lie outside regular hexagon ![]() . The first is tangent to
. The first is tangent to ![]() , and the second is tangent to
, and the second is tangent to ![]() . Both are tangent to lines
. Both are tangent to lines ![]() and
and ![]() . What is the ratio of the area of the second circle to that of the first circle?
. What is the ratio of the area of the second circle to that of the first circle?
![]()
Solution 1
A good diagram is very helpful.
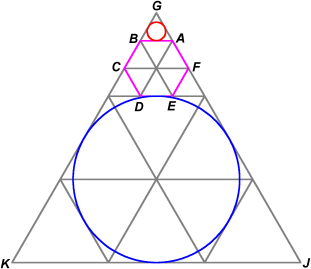
The first circle is in red, the second in blue.
With this diagram, we can see that the first circle is inscribed in equilateral triangle ![]() while the second circle is inscribed in
while the second circle is inscribed in ![]() .
From this, it's evident that the ratio of the blue area to the red area is equal to the ratio of the areas
.
From this, it's evident that the ratio of the blue area to the red area is equal to the ratio of the areas ![]() to
to ![]()
Since the ratio of areas is equal to the square of the ratio of lengths, we know our final answer is ![]() .
From the diagram, we can see that this is
.
From the diagram, we can see that this is ![]()
Solution 2
As above, we note that the first circle is inscribed in an equilateral triangle of side length ![]() (if we assume, WLOG, that the regular hexagon has side length
(if we assume, WLOG, that the regular hexagon has side length ![]() ). The inradius of an equilateral triangle with side length
). The inradius of an equilateral triangle with side length ![]() is equal to
is equal to ![]() . Therefore, the area of the first circle is
. Therefore, the area of the first circle is ![]() .
.
Call the center of the second circle ![]() . Now we drop a perpendicular from
. Now we drop a perpendicular from ![]() to circle
to circle ![]() 's point of tangency with
's point of tangency with ![]() and draw another line connecting
and draw another line connecting ![]() to
to ![]() . Note that because triangle
. Note that because triangle ![]() is equilateral,
is equilateral, ![]() .
. ![]() bisects
bisects ![]() , so we have a
, so we have a ![]() triangle.
triangle.
Call the radius of circle ![]()
![]() .
.
![]()
The height of an equilateral triangle of side length ![]() is
is ![]() . The height of a regular hexagon of side length
. The height of a regular hexagon of side length ![]() is
is ![]() . Therefore,
. Therefore,
![]() .
.
We can now set up the following equation:
![]()
![]()
![]()
The area of Circle ![]() equals
equals ![]()
Therefore, the ratio of the areas is ![]()
Video Solution
https://youtu.be/FQO-0E2zUVI?t=1381
~IceMatrix
See Also
| 2010 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 19 |
Followed by Problem 21 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









