2011 JBMO Problems/Problem 3
Problem
Let ![]() be a positive integer. Equilateral triangle ABC is divided into
be a positive integer. Equilateral triangle ABC is divided into ![]() smaller congruent equilateral triangles (with sides parallel to its sides). Let
smaller congruent equilateral triangles (with sides parallel to its sides). Let ![]() be the number of rhombuses that contain two small equilateral triangles and
be the number of rhombuses that contain two small equilateral triangles and ![]() the number of rhombuses that contain eight small equilateral triangles. Find the difference
the number of rhombuses that contain eight small equilateral triangles. Find the difference ![]() in terms of
in terms of ![]() .
.
Solution
First we will show that the side lengths of the small triangles are ![]() of the original length. Then we can count the two rhombuses.
of the original length. Then we can count the two rhombuses.
Lemma: Small Triangle is ![]() Length of Original Triangle
Length of Original Triangle
Let the side length of the triangle be ![]() , so the total area is
, so the total area is ![]() .
.
Since the big triangle is divided into ![]() congruent equilateral triangles, the area of each smaller equilateral triangle is
congruent equilateral triangles, the area of each smaller equilateral triangle is
![]()
![]() Thus, the length of each smaller triangle is
Thus, the length of each smaller triangle is ![]()
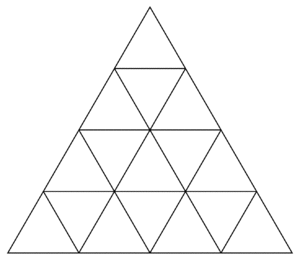
Since the lengths of each smaller triangle is ![]() and are parallel to the big triangle’s sides, the triangles are arranged like the below diagram. In diagram,
and are parallel to the big triangle’s sides, the triangles are arranged like the below diagram. In diagram, ![]() . Now we can count the rhombuses.
. Now we can count the rhombuses.
After dividing the triangles, for each line that is not in the border of the big equilateral triangle, there are two smaller equilateral triangles. The longest row in the triangle has ![]() lines and the shortest row has
lines and the shortest row has ![]() line. Thus, there are
line. Thus, there are ![]() lines parallel to one side, resulting in a total of
lines parallel to one side, resulting in a total of ![]() lines or rhombuses with 2 equilateral triangles.
lines or rhombuses with 2 equilateral triangles.
For a rhombus to have eight triangles, the center line must have two lines and the rows above and below must have one line. We can count the number of segments made of two lines that are not in the last row in the big triangle. The second longest row in the triangle has ![]() lines, while the second shortest row has
lines, while the second shortest row has ![]() lines. Thus, there are
lines. Thus, there are ![]() valid segments from two lines parallel to one side, resulting in a total of
valid segments from two lines parallel to one side, resulting in a total of ![]() rhombuses with 8 equilateral triangles.
rhombuses with 8 equilateral triangles.
Because ![]() and
and ![]() ,
,

See Also
| 2011 JBMO (Problems • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 | ||
| All JBMO Problems and Solutions | ||