2016 IMO Problems/Problem 1
Contents
[hide]Problem
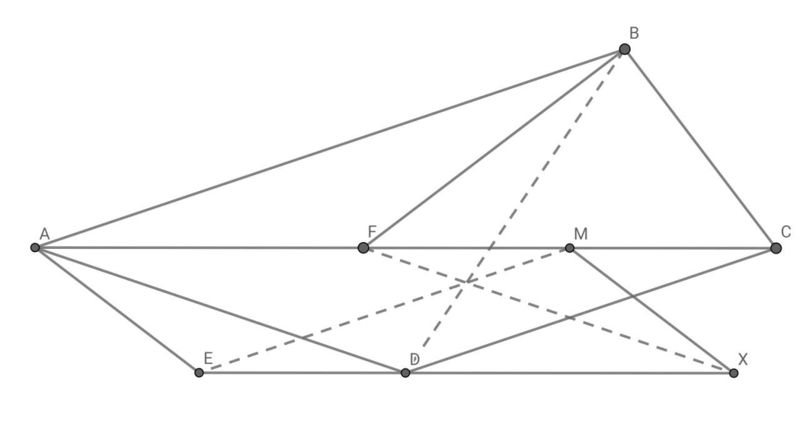
Triangle ![]() has a right angle at
has a right angle at ![]() . Let
. Let ![]() be the point on line
be the point on line ![]() such that
such that ![]() and
and ![]() lies between
lies between ![]() and
and ![]() . Point
. Point ![]() is chosen so that
is chosen so that ![]() and
and ![]() is the bisector of
is the bisector of ![]() . Point
. Point ![]() is chosen so that
is chosen so that ![]() and
and ![]() is the bisector of
is the bisector of ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() . Let
. Let ![]() be the point such that
be the point such that ![]() is a parallelogram. Prove that
is a parallelogram. Prove that ![]() and
and ![]() are concurrent.
are concurrent.
Solution
The Problem shows that
And
Finally
Solution 2
Let ![]() . And WLOG,
. And WLOG, ![]() . Hence,
. Hence, ![]() ,
,
![]()
![]() ,
,
![]()
![]() and
and
![]()
![]() .
.
So ![]() which means
which means ![]() ,
, ![]() ,
, ![]() and
and ![]() are concyclic. We know that
are concyclic. We know that ![]() and
and ![]() , so we conclude
, so we conclude ![]() is parallelogram. So
is parallelogram. So ![]() . That means
. That means ![]() is isosceles trapezoid. Hence,
is isosceles trapezoid. Hence, ![]() . By basic angle chasing,
. By basic angle chasing,
![]() and
and ![]() and we have seen that
and we have seen that ![]() , so
, so ![]() is isosceles trapezoid. And we know that
is isosceles trapezoid. And we know that ![]() bisects
bisects ![]() , so
, so ![]() is the symmetrical axis of
is the symmetrical axis of ![]() .
.
![]() and
and ![]() ,
, ![]() and
and ![]() are symmetrical respect to
are symmetrical respect to ![]() . Hence, the symmetry of
. Hence, the symmetry of ![]() with respect to
with respect to ![]() is
is ![]() . And we are done
. And we are done ![]() .
.
~EgeSaribas
See Also
| 2016 IMO (Problems) • Resources | ||
| Preceded by First Problem |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 2 |
| All IMO Problems and Solutions | ||