2019 USAMO Problems/Problem 2
Contents
[hide]Problem
Let ![]() be a cyclic quadrilateral satisfying
be a cyclic quadrilateral satisfying ![]() . The diagonals of
. The diagonals of ![]() intersect at
intersect at ![]() . Let
. Let ![]() be a point on side
be a point on side ![]() satisfying
satisfying ![]() . Show that line
. Show that line ![]() bisects
bisects ![]() .
.
Solution
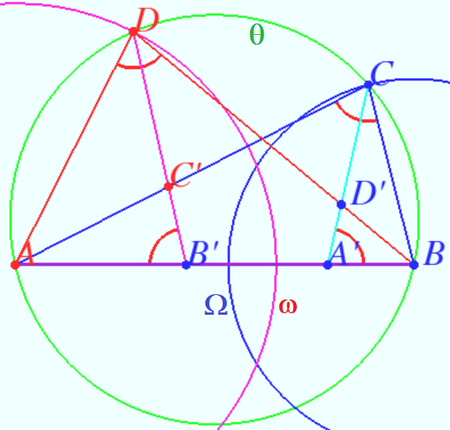
Let ![]() . Also, let
. Also, let ![]() be the midpoint of
be the midpoint of ![]() .
Note that only one point
.
Note that only one point ![]() satisfies the given angle condition. With this in mind, construct
satisfies the given angle condition. With this in mind, construct ![]() with the following properties:
with the following properties:
(1) ![]()
(2) ![]()
Claim: ![]()
Proof:
The conditions imply the similarities ![]() and
and ![]() whence
whence ![]() as desired.
as desired. ![]()
Claim: ![]() is a symmedian in
is a symmedian in ![]()
Proof:
We have
 as desired.
as desired. ![]()
Since ![]() is the isogonal conjugate of
is the isogonal conjugate of ![]() ,
, ![]() . However
. However ![]() implies that
implies that ![]() is the midpoint of
is the midpoint of ![]() from similar triangles, so we are done.
from similar triangles, so we are done. ![]()
Solution 2
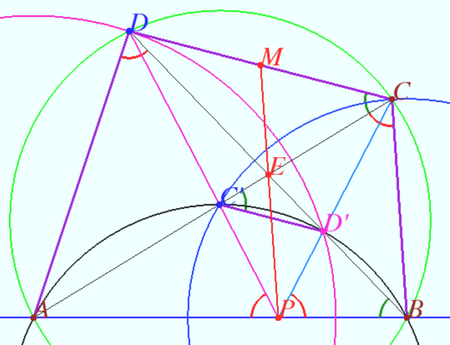
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
We denote ![]() and
and ![]() inversion with respect to
inversion with respect to ![]() and
and ![]() respectively.
respectively.
![]()
![]()
![]()
![]() Let
Let ![]() be the circle
be the circle ![]()
![]() straight line, therefore
straight line, therefore ![]()
![]() straight line, therefore
straight line, therefore
![]()
![]() is cyclic
is cyclic ![]()
![]() points
points ![]() and
and ![]() are coincide.
are coincide.
Denote ![]()
Suppose, we move point ![]() from
from ![]() to
to ![]() Then
Then ![]() decreases monotonically,
decreases monotonically, ![]() increases monotonically. So, there is only one point where
increases monotonically. So, there is only one point where ![]()
![]()
![]() is cyclic.
is cyclic.
![]()
![]() is trapezoid.
is trapezoid.
It is known that the intersection of the diagonals, intersection point of the lines containing the lateral sides of the trapezoid and the midpoints of two parallel sides are collinear.
vladimir.shelomovskii@gmail.com, vvsss
See also
| 2019 USAMO (Problems • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()