2020 USAMO Problems/Problem 1
Problem 1
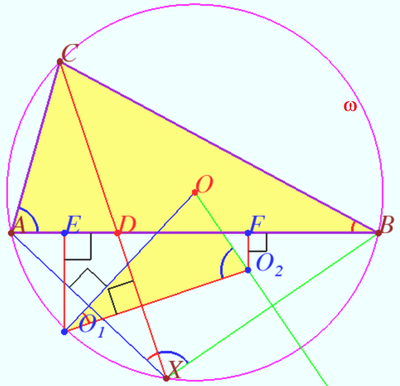
Let ![]() be a fixed acute triangle inscribed in a circle
be a fixed acute triangle inscribed in a circle ![]() with center
with center ![]() . A variable point
. A variable point ![]() is chosen on minor arc
is chosen on minor arc ![]() of
of ![]() , and segments
, and segments ![]() and
and ![]() meet at
meet at ![]() . Denote by
. Denote by ![]() and
and ![]() the circumcenters of triangles
the circumcenters of triangles ![]() and
and ![]() , respectively. Determine all points
, respectively. Determine all points ![]() for which the area of triangle
for which the area of triangle ![]() is minimized.
is minimized.
Solution
Let ![]() be midpoint
be midpoint ![]() Let
Let ![]() be midpoint
be midpoint ![]()
![]()
![]() and
and ![]() are the bases of perpendiculars dropped from
are the bases of perpendiculars dropped from ![]() and
and ![]() respectively.
respectively.
Therefore ![]()
![]()
![]() is cyclic)
is cyclic) ![]()
Similarly ![]()
The area of ![]() is minimized if
is minimized if ![]() because
because
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
https://www.youtube.com/watch?v=m157cfw0vdE
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()