2021 JMPSC Invitationals Problems/Problem 12
Contents
[hide]Problem
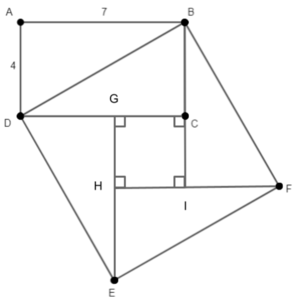
Rectangle ![]() is drawn such that
is drawn such that ![]() and
and ![]() .
. ![]() is a square that contains vertex
is a square that contains vertex ![]() in its interior. Find
in its interior. Find ![]() .
.
Solution 1 (Clever Construction)
We draw a line from ![]() to point
to point ![]() on
on ![]() such that
such that ![]() . We then draw a line from
. We then draw a line from ![]() to point
to point ![]() on
on ![]() such that
such that ![]() . Finally, we extend
. Finally, we extend ![]() to point
to point ![]() on
on ![]() such that
such that ![]() .
.
Next, if we mark ![]() as
as ![]() , we know that
, we know that ![]() , and
, and ![]() . We repeat this, finding
. We repeat this, finding ![]() , so by AAS congruence,
, so by AAS congruence, ![]() . This means
. This means ![]() , and
, and ![]() , so
, so ![]() . We see
. We see ![]() , while
, while ![]() . Thus,
. Thus, ![]() ~Bradygho
~Bradygho
Solution 2 (Trig)
Let ![]() . We have
. We have ![]() , and
, and ![]() . Now, Law Of cosines on
. Now, Law Of cosines on ![]() and
and ![]() gets
gets ![]() and
and ![]() , so
, so ![]() ~ Geometry285
~ Geometry285
Solution 3 (Mass points and Ptolemy)
Let ![]() be the center of square
be the center of square ![]() . Applying moment of inertia to the system of mass points
. Applying moment of inertia to the system of mass points ![]() (which has center of mass
(which has center of mass ![]() ) gives
) gives ![]() Since
Since ![]() is a right triangle, we may further cancel out some terms via Pythag to get
is a right triangle, we may further cancel out some terms via Pythag to get ![]() To compute
To compute ![]() , apply Ptolemy to cyclic quadrilateral
, apply Ptolemy to cyclic quadrilateral ![]() (using the fact that
(using the fact that ![]() is 45-45-90) to get
is 45-45-90) to get ![]() . Thus
. Thus ![]() ~djmathman
~djmathman
See also
- Other 2021 JMPSC Invitationals Problems
- 2021 JMPSC Invitationals Answer Key
- All JMPSC Problems and Solutions
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.