2021 JMPSC Invitationals Problems/Problem 2
Contents
[hide]Problem
Two quadrilaterals are drawn on the plane such that they share no sides. What is the maximum possible number of intersections of the boundaries of the two quadrilaterals?
Solution
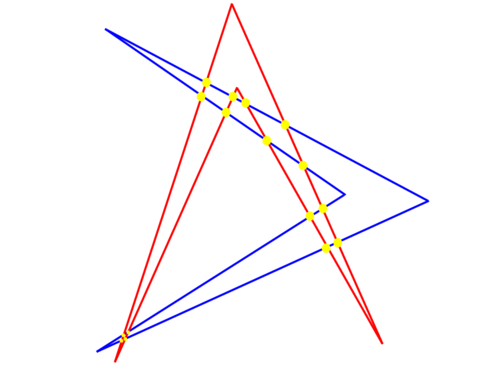
We find that it is possible to construct the maximal ![]() points, where each side of one quadrilateral intersects all four sides of the other quadrilateral.
points, where each side of one quadrilateral intersects all four sides of the other quadrilateral.
~samrocksnature
Solution 2
Take two concave quadrilaterals. Call two lines "somewhat parallel" if the different in their slopes is less than ![]() . An arrow has approximately
. An arrow has approximately ![]() lines which are "somewhat" parallel, which means
lines which are "somewhat" parallel, which means ![]() arrows that are
arrows that are ![]() to each other form
to each other form ![]() intersections.
intersections.
![]() ~Geometry285
~Geometry285
Solution 3
A line can intersect ![]() other non-parallel lines
other non-parallel lines ![]() times. If we draw
times. If we draw ![]() quadrilaterals with non-parallel sides, it would then be possible to get
quadrilaterals with non-parallel sides, it would then be possible to get ![]() intersections.
intersections.
~Mathdreams
See also
- Other 2021 JMPSC Invitationals Problems
- 2021 JMPSC Invitationals Answer Key
- All JMPSC Problems and Solutions
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.