2024 AIME II Problems/Problem 10

Problem

Let $\triangle ABC$ have circumcenter $O$ and incenter $I$ with $\overline{IA}\perp\overline{OI}$ , circumradius $13$ , and inradius $6$ . Find $AB\cdot AC$ .

Solution 1 (Similar Triangles and PoP)

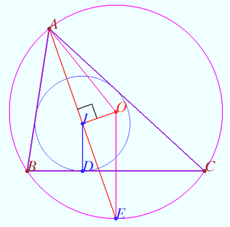
Start off by (of course) drawing a diagram! Let $I$ and $O$ be the incenter and circumcenters of triangle $ABC$ , respectively. Furthermore, extend $AI$ to meet $BC$ at $L$ and the circumcircle of triangle $ABC$ at $D$ .

$[asy] size(300); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26); pair A = (c/3,8.65*c/10); draw(circumcircle(A,B,C)); pair I=incenter(A,B,C); pair O=circumcenter(A,B,C); pair L=extension(A,I,C,B); dot(I^^O^^A^^B^^C^^D^^L); draw(A--L); draw(A--D); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(C--B--D--cycle); draw(A--C--B); draw(A--B); draw(B--I--C^^A--I); draw(incircle(A,B,C)); label("$B$",B,SW); label("$C$",C,SE); label("$A$",A,N); label("$D$",D,S); label("$I$",I,NW); label("$L$",L,SW); label("$O$",O,E); label("$\alpha$",B,5*dir(midangle(A,B,I)),fontsize(8)); label("$\alpha$",B,5*dir(midangle(I,B,C)),fontsize(8)); label("$\beta$",C,12*dir(midangle(B,C,I)),fontsize(8)); label("$\beta$",C,12*dir(midangle(I,C,A)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); draw(I--O); draw(A--O); draw(rightanglemark(A,I,O)); [/asy]$

We'll tackle the initial steps of the problem in two different manners, both leading us to the same final calculations.

Solution 1.1

Since $I$ is the incenter, $\angle BAL \cong \angle DAC$ . Furthermore, $\angle ABC$ and $\angle ADC$ are both subtended by the same arc $AC$ , so $\angle ABC \cong \angle ADC.$ Therefore by AA similarity, $\triangle ABL \sim \triangle ADC$ . From this we can say that $\frac{AB}{AD} = \frac{AL}{AC} \implies AB \cdot AC = AL \cdot AD$

Since $AD$ is a chord of the circle and $OI$ is a perpendicular from the center to that chord, $OI$ must bisect $AD$ . This can be seen by drawing $OD$ and recognizing that this creates two congruent right triangles. Therefore, $AD = 2 \cdot ID \implies AB \cdot AC = 2 \cdot AL \cdot ID$

We have successfully represented $AB \cdot AC$ in terms of $AL$ and $ID$ . Solution 1.2 will explain an alternate method to get a similar relationship, and then we'll rejoin and finish off the solution.

Solution 1.2

$\angle ALB \cong \angle DLC$ by vertical angles and $\angle LBA \cong \angle CDA$ because both are subtended by arc $AC$ . Thus $\triangle ABL \sim \triangle CDL$ .

Thus $\frac{AB}{CD} = \frac{AL}{CL} \implies AB = CD \cdot \frac{AL}{CL}$

Symmetrically, we get $\triangle ALC \sim \triangle BLD$ , so $\frac{AC}{BD} = \frac{AL}{BL} \implies AC = BD \cdot \frac{AL}{BL}$

Substituting, we get $AB \cdot AC = CD \cdot \frac{AL}{CL} \cdot BD \cdot \frac{AL}{BL}$

Lemma 1: BD = CD = ID

Proof:

We commence angle chasing: we know $\angle DBC \cong DAC = \gamma$ . Therefore $\angle IBD = \alpha + \gamma$ . Looking at triangle $ABI$ , we see that $\angle IBA = \alpha$ , and $\angle BAI = \gamma$ . Therefore because the sum of the angles must be $180$ , $\angle BIA = 180-\alpha - \gamma$ . Now $AD$ is a straight line, so $\angle BID = 180-\angle BIA = \alpha+\gamma$ . Since $\angle IBD = \angle BID$ , triangle $IBD$ is isosceles and thus $ID = BD$ .

A similar argument should suffice to show $CD = ID$ by symmetry, so thus $ID = BD = CD$ .

Now we regroup and get $CD \cdot \frac{AL}{CL} \cdot BD \cdot \frac{AL}{BL} = ID^2 \cdot \frac{AL^2}{BL \cdot CL}$

Now note that $BL$ and $CL$ are part of the same chord in the circle, so we can use Power of a point to express their product differently. $BL \cdot CL = AL \cdot LD \implies AB \cdot AC = ID^2 \cdot \frac{AL}{LD}$

Solution 1 (Continued)

Now we have some sort of expression for $AB \cdot AC$ in terms of $ID$ and $AL$ . Let's try to find $AL$ first.

Drop an altitude from $D$ to $BC$ , $I$ to $AC$ , and $I$ to $BC$ :

$[asy] size(300); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26), E = (c/2-0.01,0); pair A = (c/3,8.65*c/10); pair F = (2*c/3-0.14, 4-0.29); pair G = (c/2-0.68,0); draw(circumcircle(A,B,C)); pair I=incenter(A,B,C); pair O=circumcenter(A,B,C); pair L=extension(A,I,C,B); dot(I^^O^^A^^B^^C^^D^^L^^E^^F^^G); draw(A--L); draw(A--D); draw(D--E); draw(I--F); draw(I--G); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(C--B--D--cycle); draw(A--C--B); draw(A--B); draw(B--I--C^^A--I); draw(incircle(A,B,C)); label("$B$",B,SW); label("$C$",C,SE); label("$A$",A,N); label("$D$",D,S); label("$I$",I,NW); label("$L$",L,SW); label("$O$",O,E); label("$E$",E,N); label("$F$",F,NE); label("$G$",G,SW); label("$\alpha$",B,5*dir(midangle(A,B,I)),fontsize(8)); label("$\alpha$",B,5*dir(midangle(I,B,C)),fontsize(8)); label("$\beta$",C,12*dir(midangle(B,C,I)),fontsize(8)); label("$\beta$",C,12*dir(midangle(I,C,A)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); draw(I--O); draw(A--O); draw(rightanglemark(A,I,O)); draw(rightanglemark(B,E,D)); draw(rightanglemark(I,F,A)); draw(rightanglemark(I,G,L)); [/asy]$

Since $\angle DBE \cong \angle IAF$ and $\angle BED \cong \angle IFA$ , $\triangle BDE \sim \triangle AIF$ .

Furthermore, we know $BD = ID$ and $AI = ID$ , so $BD = AI$ . Since we have two right similar triangles and the corresponding sides are equal, these two triangles are actually congruent: this implies that $DE = IF = 6$ since $IF$ is the inradius.

Now notice that $\triangle IGL \sim \triangle DEL$ because of equal vertical angles and right angles. Furthermore, $IG$ is the inradius so it's length is $6$ , which equals the length of $DE$ . Therefore these two triangles are congruent, so $IL = DL$ .

Since $IL+DL = ID$ , $ID = 2 \cdot IL$ . Furthermore, $AL = AI + IL = ID + IL = 3 \cdot IL$ .

We can now plug back into our initial equations for $AB \cdot AC$ :

From $1.1$ , $AB \cdot AC = 2 \cdot AL \cdot ID = 2 \cdot 3 \cdot IL \cdot 2 \cdot IL$

$\implies AB \cdot AC = 3 \cdot (2 \cdot IL) \cdot (2 \cdot IL) = 3 \cdot ID^2$

Alternatively, from $1.2$ , $AB \cdot AC = ID^2 \cdot \frac{AL}{DL}$ $\implies AB \cdot AC = ID^2 \cdot \frac{3 \cdot IL}{IL} = 3 \cdot ID^2$

Now all we need to do is find $ID$ .

The problem now becomes very simple if one knows Euler's Formula for the distance between the incenter and the circumcenter of a triangle. This formula states that $OI^2 = R(R-2r)$ , where $R$ is the circumradius and $r$ is the inradius. We will prove this formula first, but if you already know the proof, skip this part.

Theorem: in any triangle, let $d$ be the distance from the circumcenter to the incenter of the triangle. Then $d^2 = R \cdot (R-2r)$ , where $R$ is the circumradius of the triangle and $r$ is the inradius of the triangle.

Proof:

Construct the following diagram:

$[asy] size(300); import olympiad; real c=8.1,a=5*(c+sqrt(c^2-64))/6,b=5*(c-sqrt(c^2-64))/6; pair B=(0,0),C=(c,0), D = (c/2-0.01, -2.26), E = (c/2-0.01,0); pair A = (c/3,8.65*c/10); pair F = (2*c/3-0.14, 4-0.29); pair G = (c/2-0.68,0); draw(circumcircle(A,B,C)); pair I=incenter(A,B,C); pair O=circumcenter(A,B,C); pair L=extension(A,I,C,B); dot(I^^O^^A^^B^^C^^D^^L^^F); draw(A--L); draw(A--D); draw(I--F); path midangle(pair d,pair e,pair f) {return e--e+((f-e)/length(f-e)+(d-e)/length(d-e))/2;} draw(C--B--D--cycle); draw(A--C--B); draw(A--B); draw(A--I); draw(incircle(A,B,C)); label("$B$",B,SW); label("$C$",C,SE); label("$A$",A,N); label("$D$",D,S); label("$I$",I,NW); label("$L$",L,SW); label("$O$",O,S); label("$F$",F,NE); label("$\gamma$",A,5*dir(midangle(B,A,I)),fontsize(8)); label("$\gamma$",A,5*dir(midangle(I,A,C)),fontsize(8)); pair H = (10*c/8-1.46,2*c/3-1.85), J = (-0.55,1.4); dot(H^^J); label("$H$", H, E); label("$J$", J, W); draw(I--O); draw(I--H); draw(I--J); draw(rightanglemark(I,F,A)); [/asy]$

Let $OI = d$ , $OH = R$ , $IF = r$ . By the Power of a Point, $IH \cdot IJ = AI \cdot ID$ . $IH = R+d$ and $IJ = R-d$ , so $(R+d) \cdot (R-d) = AI \cdot ID = AI \cdot CD$

Now consider $\triangle ACD$ . Since all three points lie on the circumcircle of $\triangle ABC$ , the two triangles have the same circumcircle. Thus we can apply law of sines and we get $\frac{CD}{\sin(\angle DAC)} = 2R$ . This implies

$(R+d)\cdot (R-d) = AI \cdot 2R \cdot \sin(\angle DAC)$

Also, $\sin(\angle DAC)) = \sin(\angle IAF))$ , and $\triangle IAF$ is right. Therefore $\sin(\angle IAF) = \frac{IF}{AI} = \frac{r}{AI}$

Plugging in, we have

$(R+d)\cdot (R-d) = AI \cdot 2R \cdot \frac{r}{AI} = 2R \cdot r$

Thus $R^2-d^2 = 2R \cdot r \implies d^2 = R \cdot (R-2r)$

Now we can finish up our solution. We know that $AB \cdot AC = 3 \cdot ID^2$ . Since $ID = AI$ , $AB \cdot AC = 3 \cdot AI^2$ . Since $\triangle AOI$ is right, we can apply the pythagorean theorem: $AI^2 = AO^2-OI^2 = 13^2-OI^2$ .

Plugging in from Euler's formula, $OI^2 = 13 \cdot (13 - 2 \cdot 6) = 13$ .

Thus $AI^2 = 169-13 = 156$ .

Finally $AB \cdot AC = 3 \cdot AI^2 = 3 \cdot 156 = \textbf{468}$ .

~KingRavi

Solution 2 (Excenters)

By Euler's formula $OI^{2}=R(R-2r)$ , we have $OI^{2}=13(13-12)=13$ . Thus, by the Pythagorean theorem, $AI^{2}=13^{2}-13=156$ . Let $AI\cap(ABC)=M$ ; notice $\triangle AOM$ is isosceles and $\overline{OI}\perp\overline{AM}$ which is enough to imply that $I$ is the midpoint of $\overline{AM}$ , and $M$ itself is the midpoint of $II_{a}$ where $I_{a}$ is the $A$ -excenter of $\triangle ABC$ . Therefore, $AI=IM=MI_{a}=\sqrt{156}$ and $AB\cdot AC=AI\cdot AI_{a}=3\cdot AI^{2}=\boxed{468}.$

Note that this problem is extremely similar to 2019 CIME I/14.

Solution 3

Denote $AB=a, AC=b, BC=c$ . By the given condition, $\frac{abc}{4A}=13; \frac{2A}{a+b+c}=6$ , where $A$ is the area of $\triangle{ABC}$ .

Moreover, since $OI\bot AI$ , the second intersection of the line $AI$ and $(ABC)$ is the reflection of $A$ about $I$ , denote that as $D$ . By the incenter-excenter lemma, $DI=BD=CD=\frac{AD}{2}\implies BD(a+b)=2BD\cdot c\implies a+b=2c$ .

Thus, we have $\frac{2A}{a+b+c}=\frac{2A}{3c}=6, A=9c$ . Now, we have $\frac{abc}{4A}=\frac{abc}{36c}=\frac{ab}{36}=13\implies ab=\boxed{468}$

~Bluesoul

Solution 4 (Trig)

Denote by $R$ and $r$ the circumradius and inradius, respectively.

First, we have $r = 4 R \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} \hspace{1cm} (1)$

Second, because $AI \perp IO$ , \begin{align*} AI & = AO \cos \angle IAO \\ & = AO \cos \left( 90^\circ - C - \frac{A}{2} \right) \\ & = AO \sin \left( C + \frac{A}{2} \right) \\ & = R \sin \left( C + \frac{180^\circ - B - C}{2} \right) \\ & = R \cos \frac{B - C}{2} . \end{align*}

Thus, \begin{align*} r & = AI \sin \frac{A}{2} \\ & = R \sin \frac{A}{2} \cos \frac{B-C}{2} \hspace{1cm} (2) \end{align*}

Taking $(1) - (2)$ , we get \[ 4 \sin \frac{B}{2} \sin \frac{C}{2} = \cos \frac{B-C}{2} . \]

We have \begin{align*} 2 \sin \frac{B}{2} \sin \frac{C}{2} & = - \cos \frac{B+C}{2} + \cos \frac{B-C}{2} . \end{align*}

Plugging this into the above equation, we get \[ \cos \frac{B-C}{2} = 2 \cos \frac{B+C}{2} . \hspace{1cm} (3) \]

Now, we analyze Equation (2). We have \begin{align*} \frac{r}{R} & = \sin \frac{A}{2} \cos \frac{B-C}{2} \\ & = \sin \frac{180^\circ - B - C}{2} \cos \frac{B-C}{2} \\ & = \cos \frac{B+C}{2} \cos \frac{B-C}{2} \hspace{1cm} (4) \end{align*}

Solving Equations (3) and (4), we get \[ \cos \frac{B+C}{2} = \sqrt{\frac{r}{2R}}, \hspace{1cm} \cos \frac{B-C}{2} = \sqrt{\frac{2r}{R}} . \hspace{1cm} (5) \]

Now, we compute $AB \cdot AC$ . We have \begin{align*} AB \cdot AC & = 2R \sin C \cdot 2R \sin B \\ & = 2 R^2 \left( - \cos \left( B + C \right) + \cos \left( B - C \right) \right) \\ & = 2 R^2 \left( - \left( 2 \left( \cos \frac{B+C}{2} \right)^2 - 1 \right) + \left( 2 \left( \cos \frac{B-C}{2} \right)^2 - 1 \right) \right) \\ & = 6 R r \\ & = \boxed{\textbf{(468) }} \end{align*} where the first equality follows from the law of sines, the fourth equality follows from (5).

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Solution 5 (Trig)

Firstly, we can construct the triangle $\triangle ABC$ by drawing the circumcirlce (centered at $O$ with radius $R = OA = 13$ ) and incircle (centered at $I$ with radius $r = 6$ ). Next, from $A$ , construct tangent lines to the incircle meeting the circumcirlce at point $B$ and $C$ , say, as shown in the diagram. By Euler's theorem (relating the distance between $O$ and $I$ to the circumradius and inradius), we have $OI = \sqrt{R^2 - 2rR} = \sqrt{13}.$ This leads to $AI = \sqrt{R^2 - OI^2} = \sqrt{156}.$ Let $P$ be the point of tangency where the incircle meets the side $\overline{AC}$ . Now we denote $\theta \coloneqq \angle BAI = \angle IAP \qquad \text{and} \qquad \phi \coloneqq \angle OAI.$ Notice that $\angle BAO = \angle BAI - \angle OAI = \theta - \phi$ . Finally, the crux move is to recognize $AB = 2R \cos(\theta - \phi) \qquad \text{and} \qquad AC = 2R \cos(\theta + \phi)$ since $O$ is the circumcenter. Then multiply these two expressions and apply the compound-angle formula to get \begin{aligned} AB \cdot AC &= 4R^2 \cos(\theta - \phi) \cos(\theta + \phi) \\[0.3em] &= 4R^2\left( \cos^2\theta \cos^2\phi - \sin^2\theta \sin^2\phi \right) \\[0.3em] &= 4\cos^2\theta(\underbrace{R\cos\phi}_{AI \, = \, \sqrt{156}})^2 - 4\sin^2\theta(\underbrace{R\sin\phi}_{OI \, = \, \sqrt{13}})^2 \\[0.3em] &= 52 (12\cos^2\theta - \sin^2 \theta) \\[0.3em] AB \cdot AC &= 52 (12 - 13\sin^2\theta), \end{aligned} where in the last equality, we make use of the substitution $\cos^2\theta = 1 - \sin^2\theta$ . Looking at $\triangle AIP$ , we learn that $\sin \theta = \frac{r}{AI} = \frac{6}{\sqrt{156}}$ which means $\sin^2 \theta = \frac{3}{13}$ . Hence we have $AB \cdot AC = 52\left( 12 - 13 \cdot \tfrac{3}{13} \right) = 52 \cdot 9 = \boxed{468}.$ This completes the solution

-- VensL.

Solution 6 (Close to Solution 3)

Denote $E = \odot ABC \cap AI, AB = c, AC = b, BC=a, r$ is inradius.

$AO = EO = R \implies AI = EI.$

It is known that $\frac {AI}{EI} = \frac {b+c}{a} – 1 = 1 \implies b + c = 2a.$ Points on bisectors

$[ABC] =\frac{ (a+b+c) r}{2} = \frac {3ar}{2} = \frac {abc}{4R} \implies bc = 6Rr = \boxed{468}.$ vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://youtu.be/_zxBvojcAQ4

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

Video Solution

https://www.youtube.com/watch?v=pPBPfpo12j4

~MathProblemSolvingSkills.com

2024 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 9	Followed by Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search

2024 AIME II Problems/Problem 10

Contents

Problem

Solution 1 (Similar Triangles and PoP)

Solution 1.1

Solution 1.2

Solution 1 (Continued)

Solution 2 (Excenters)

Solution 3

Solution 4 (Trig)

Solution 5 (Trig)

Solution 6 (Close to Solution 3)

Video Solution

Video Solution

See also