2024 AMC 12B Problems/Problem 13
Contents
[hide]Problem 13
There are real numbers ![]() and
and ![]() that satisfy the system of equations
that satisfy the system of equations![]()
![]() What is the minimum possible value of
What is the minimum possible value of ![]() ?
?
![]()
Solution 1 (Easy and Fast)
Adding up the first and second equation, we get:
 All squared values must be greater than or equal to
All squared values must be greater than or equal to ![]() . As we are aiming for the minimum value, we set the two squared terms to be
. As we are aiming for the minimum value, we set the two squared terms to be ![]() .
.
This leads to ![]()
~mitsuihisashi14
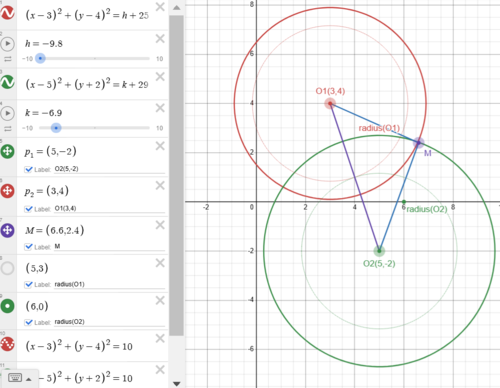
Solution 2 (Coordinate Geometry and AM-GM Inequality)
![]()
![]() The distance between 2 circle centers is
The distance between 2 circle centers is ![]() The 2 circles must intersect given there exists one or more pairs of (x,y), connecting
The 2 circles must intersect given there exists one or more pairs of (x,y), connecting ![]() and any pair of the 2 circle intersection points gives us a triangle with 3 sides, then
and any pair of the 2 circle intersection points gives us a triangle with 3 sides, then
![]()
![]() Note that they will be equal if and only if the circles are tangent,
Note that they will be equal if and only if the circles are tangent,
Applying the AM-GM inequality (![]() ) in the steps below, we get
) in the steps below, we get
![\[h + k + 54 = (h + 25) + (k + 29) =\sqrt{(h + 25)}^2 + \sqrt{(k + 29)}^2 \geq \frac{\left(\sqrt{h + 25} + \sqrt{k + 29}\right)^2}{2} \geq \frac{\left(2\sqrt{10}\right)^2}{2} = 20.\]](http://latex.artofproblemsolving.com/3/2/c/32ca303b4f306d3bb7501a1ce7113a518393722d.png)
Therefore, ![]() .
.
Solution 3
~Kathan
Video Solution 1 by SpreadTheMathLove
https://www.youtube.com/watch?v=U0PqhU73yU0
See also
| 2024 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 12 |
Followed by Problem 14 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()