2025 USAMO Problems/Problem 4
- The following problem is from both the 2025 USAMO #4 and 2025 USAJMO #5, so both problems redirect to this page.
Contents
[hide]Problem
Let ![]() be the orthocenter of acute triangle
be the orthocenter of acute triangle ![]() , let
, let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() to
to ![]() , and let
, and let ![]() be the reflection of
be the reflection of ![]() across
across ![]() . Suppose that the circumcircle of triangle
. Suppose that the circumcircle of triangle ![]() intersects line
intersects line ![]() at two distinct points
at two distinct points ![]() and
and ![]() . Prove that
. Prove that ![]() is the midpoint of
is the midpoint of ![]() .
.
Solution 1
Let AP intersects BC at D. Extend FC to the point E on the circumcircle ![]() of
of ![]() . Since
. Since ![]() is the orthocenter of
is the orthocenter of ![]() , we know that
, we know that ![]() or
or ![]() , and
, and ![]() . Next we use the power of H in
. Next we use the power of H in ![]() :
: ![]() . These relations imply that
. These relations imply that ![]() .
.
Hence ![]() are midpoints of
are midpoints of ![]() respectively. By midline theorem,
respectively. By midline theorem, ![]() . Since
. Since ![]() , we have
, we have ![]() . This implies that
. This implies that ![]() . Consequently,
. Consequently, ![]() is the diameter of
is the diameter of ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() which is also the center of
which is also the center of ![]() .
. ![]() are midpoints of
are midpoints of ![]() respectively. By the midline theorem again, we have
respectively. By the midline theorem again, we have ![]() , consequently,
, consequently, ![]() . This implies that
. This implies that ![]() is the perpendicular bisector of the chord
is the perpendicular bisector of the chord ![]() hence
hence ![]() is the midpoint of
is the midpoint of ![]() . ~ Dr. Shi davincimath.com
. ~ Dr. Shi davincimath.com
Solution 2
Denote ![]() as the center of
as the center of ![]() ,
, ![]() as the center of
as the center of ![]() ,
, ![]() as the midpoint of
as the midpoint of ![]() ,
, ![]() as the midpoint of
as the midpoint of ![]() , and
, and ![]() as the midpoint of
as the midpoint of ![]() . It suffices to show that
. It suffices to show that ![]() .
.
Claim: ![]() is cyclic.
is cyclic.
Proof: Since ![]() and
and ![]() , KM is a midline of
, KM is a midline of ![]() and
and ![]() .
. ![]() as well since
as well since ![]() , so
, so ![]() lies on
lies on ![]() .
Next, note that
.
Next, note that ![]() lies on
lies on ![]() , so the perpendicular bisector of
, so the perpendicular bisector of ![]() through
through ![]() passes through
passes through ![]() . In other words,
. In other words, ![]() , and
, and ![]() are collinear. Since
are collinear. Since ![]() and
and ![]() are both perpendicular to
are both perpendicular to ![]() , it follows that they are parallel.
Since
, it follows that they are parallel.
Since ![]() and
and ![]() , then
, then ![]() .
Finally, we have that
.
Finally, we have that ![]() and thus
and thus ![]() is cyclic. It follows that
is cyclic. It follows that ![]() , so
, so ![]() , as desired.
, as desired.
-mop
Solution 3
Connect ![]() and have
and have ![]() intersect
intersect ![]() at
at ![]() . Also extend
. Also extend ![]() past point
past point ![]() and have it intersect with the circle at point
and have it intersect with the circle at point ![]() .
.
Since ![]() is the reflection of
is the reflection of ![]() over
over ![]() , we know that
, we know that ![]() . Since
. Since ![]() is the orthocenter, we can draw the altitude and tell that
is the orthocenter, we can draw the altitude and tell that ![]() ,
, ![]() , and
, and ![]() are collinear.
We know
are collinear.
We know ![]() and
and ![]() , so
, so ![]() by AA, so
by AA, so ![]() .
.
![]() and
and ![]() . From this, we can tell that
. From this, we can tell that ![]() . Therefore,
. Therefore, ![]() and
and ![]() .
.
If we connect ![]() , we can tell that that
, we can tell that that ![]() due to
due to ![]() being the reflection of
being the reflection of ![]() and
and ![]() being perpendicular to
being perpendicular to ![]() , so
, so ![]() . In addition,
. In addition, ![]() . Also,
. Also, ![]() because they are vertical angles.
because they are vertical angles.
So, ![]() because of SAA. From this we can conclude that
because of SAA. From this we can conclude that ![]() , so
, so ![]() is the midpoint of
is the midpoint of ![]() .
.
Solution 4
Let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() to
to ![]() By Power of a Point, we have
By Power of a Point, we have
![]() and
and
![]() Adding, we get
Adding, we get
![]() It is well known that the reflection of
It is well known that the reflection of ![]() over
over ![]() which we denote by
which we denote by ![]() lies on
lies on ![]() Then, let
Then, let ![]() We have
We have
![]() Thus,
Thus, ![]() and since
and since ![]() we have
we have ![]() Hence,
Hence, ![]() is the midpoint of
is the midpoint of ![]() ~TThB0501
~TThB0501
Solution 5
Let Q be the antipode of B. Claim — AHQC is a parallelogram, and AP CQ is an isosceles trapezoid.
Proof. As AH ⊥ BC ⊥ CQ and CF ⊥ AB ⊥ AQ. Let M be the midpoint of QC.
Claim — Point M is the circumcenter of triangle AFP.
Proof. It’s clear that MA = MP from the isosceles trapezoid.
As for MA = MF, let N denote the midpoint of AF; then MN is a midline of the parallelogram, so MN ⊥ AF. Since CM ⊥ BC and M is the center of (AF P), it follows CX = CY .
Video Solution - A 2-minute proof
Solution 6
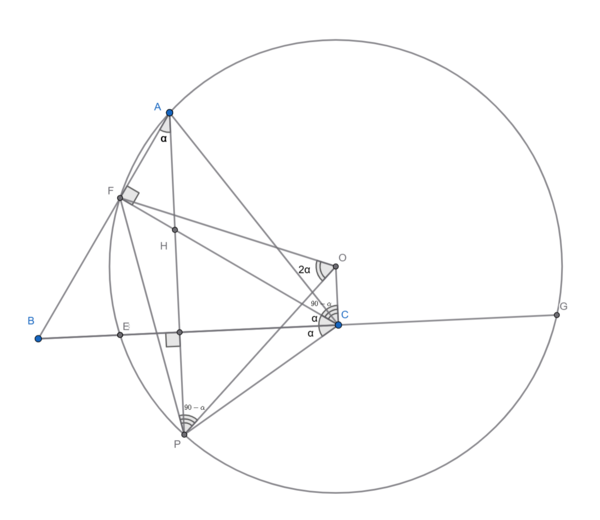
Quick angle chasing gives ![]() .
Let
.
Let ![]() be the circumcenter of
be the circumcenter of ![]() .
.
Thus ![]() (because O and A lie on the same side of segment
(because O and A lie on the same side of segment ![]() ).
).
As ![]() , the quadrilateral FOCP is cyclic.
, the quadrilateral FOCP is cyclic.
Observe that ![]() , so
, so ![]() .
.
From the properties of cyclic quadrilaterals, ![]()
Thus ![]() .
Therefore
.
Therefore ![]() is perpendicular to chord
is perpendicular to chord ![]() ,
, ![]() .
.