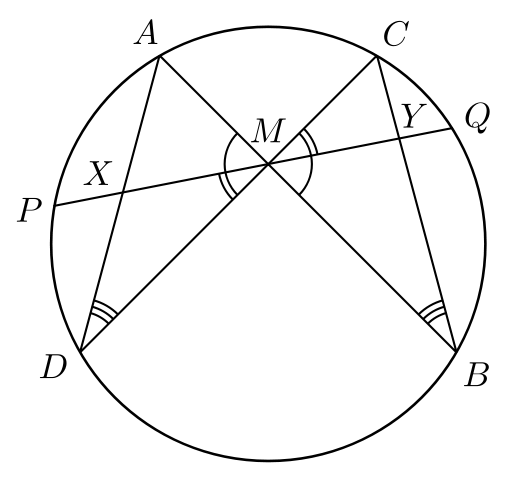
Butterfly Theorem
Let ![]() be the midpoint of chord
be the midpoint of chord ![]() of a circle, through which two other chords
of a circle, through which two other chords ![]() and
and ![]() are drawn.
are drawn. ![]() and
and ![]() intersect chord
intersect chord ![]() at
at ![]() and
and ![]() , respectively. The Butterfly Theorem states that
, respectively. The Butterfly Theorem states that ![]() is the midpoint of
is the midpoint of ![]() .
.
Proof
This simple proof uses projective geometry.
First we note that ![]() Therefore,
Therefore,
![]() Since
Since ![]() ,
,
![]() Moreover,
Moreover,
![]() so
so ![]() as desired.
as desired.
![]() .
.
Related Reading
http://agutie.homestead.com/FiLEs/GeometryButterfly.html
http://www.mathematik.uni-muenchen.de/~fritsch/butterfly.pdf