Double perspective triangles
Double perspective triangles
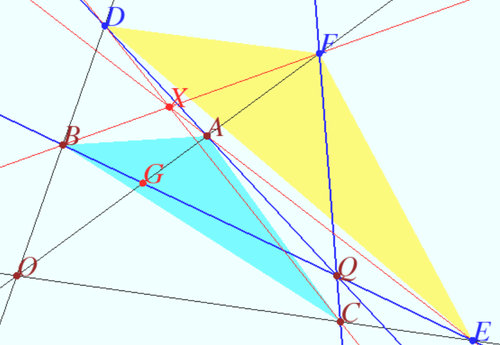
Two triangles in double perspective are in triple perspective
Let ![]() and
and ![]() be in double perspective, which means that triples of lines
be in double perspective, which means that triples of lines ![]() and
and ![]() are concurrent. Prove that lines
are concurrent. Prove that lines ![]() and
and ![]() are concurrent (the triangles are in triple perspective).
are concurrent (the triangles are in triple perspective).
Proof
Denote ![]()
It is known that there is projective transformation that maps any quadrungle into square.
We use this transformation for ![]() .
We use the Claim for square and get the result: lines
.
We use the Claim for square and get the result: lines ![]() and
and ![]() are concurrent.
are concurrent.
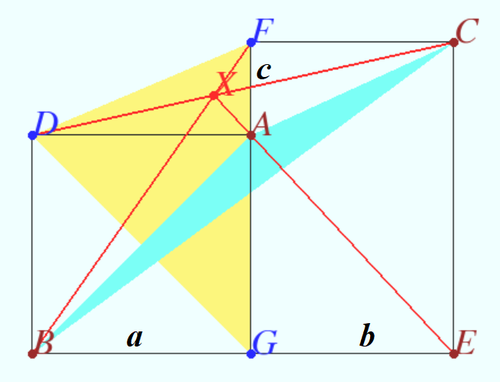
Claim for square
Let ![]() be the square, let
be the square, let ![]() be the rectangle,
be the rectangle, ![]()
Prove that lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Let ![]() Then
Then
![]()
![]()
![]()
![]() where
where ![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss