Kimberling center
C. Kimberling has extensively tabulated and enumerated the properties of triangle centers (Kimberling 1994, 1998, and online), denoting the nth center in his numbering scheme by ![]() . 101 (plus 13 additional) centers appeared in Kimberling (1994), 360 in Kimberling (1998), and the remainder appear in a list maintained online by Kimberling at http://faculty.evansville.edu/ck6/encyclopedia/ETC.html. In his honor, these centers are called Kimberling centers in this work. Kimberling's compilation contains 3053 centers as of December 2004. A subset of these is illustrated above.
. 101 (plus 13 additional) centers appeared in Kimberling (1994), 360 in Kimberling (1998), and the remainder appear in a list maintained online by Kimberling at http://faculty.evansville.edu/ck6/encyclopedia/ETC.html. In his honor, these centers are called Kimberling centers in this work. Kimberling's compilation contains 3053 centers as of December 2004. A subset of these is illustrated above.
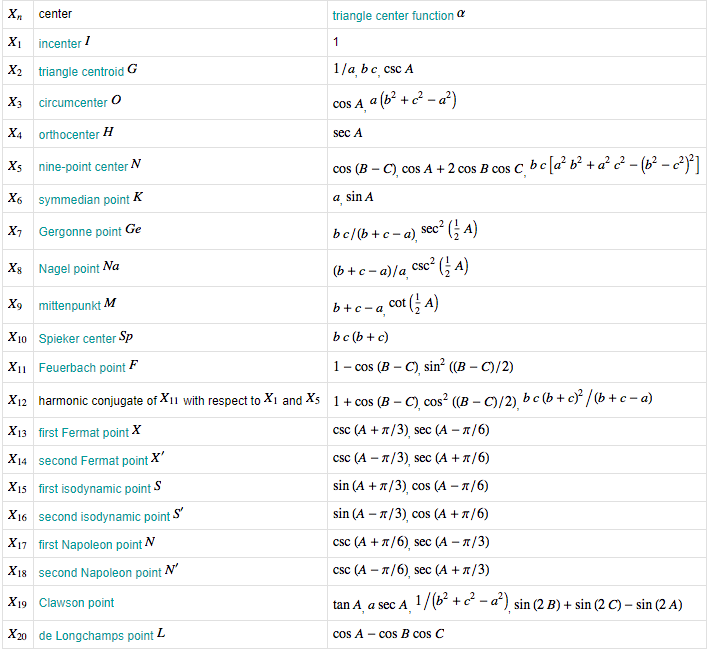
The first few Kimberling centers are summarized in the table below with their numbers, names, and trilinears.
Weisstein, Eric W. "Kimberling Center." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/KimberlingCenter.html