Art of Problem Solving

AoPS Online

MIE 96/97

Contents

1 Problem 1
2 Problem 2
3 Problem 3
4 Problem 4
5 Problem 5
6 Problem 6
7 Problem 7
8 Problem 8

Problem 1

Solve the following system

$\begin{cases}x^y=y^x\\y=ax\end{cases}~\mbox{where }a\neq1\mbox{ and }a>0$

Problem 2

Find the maximum term of the expansion of

$\left(1+\frac{1}{3}\right)^{65}$

Problem 3

Given the points $A$ and $B$ of the plane, find the equation of the geometric place of the points $P$ of the plane such that the ratio of the distances between from $P$ to $A$ and from $P$ to $B$ are given by a constant $k$ . Justify your answer discussing every possibility for $k$ .

Problem 4

On each of the six faces of a cube it has been drawn a circumference, where has been marked $n$ points. Considering that four points can't be on the same face and can't be coplanars, find how many lines and triangles, that aren't on the faces of this cube, are determined by the points.

Problem 5

Consider the function $f(x)=\ln(x+\sqrt{x^2+1})$ . Answer to the following questions:

(a) If $g(x)=\ln(2x)$ , what's the relation between the curves of $f$ and $g$ ?

(b) Can we say that the function defined by $H(x)=\frac{f(x)}{2}$ is a primitive form for the function $T(x)=\frac{f(x)}{\sqrt{x^2+1}}$ ?

Problem 6

If $\tan a$ and $\tan b$ are the roots of $x^2+px+q=0$ , then compute, in terms of $p$ and $q$ , the value of:

$\sin^2(a+b)+p\cdot\sin(a+b)\cos(a+b)+q\cdot\cos^2(a+b)$

Consider $p,q\in\mathbb{R}$ and $q\neq1$ .

Problem 7

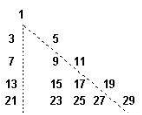
Consider the successively written odd numbers, like the following image, where the $n$ -line has $n$ numbers. Find in terms of $n$ , in this line, the sum of all written numbers.

Problem 8

Find the remainder of the division of the polynomial $(\cos\varphi+x\sin\varphi)^n$ by $(x^2+1)$ , where $n$ is a natural number.

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=MIE_96/97&oldid=89541"

© 2024 AoPS Incorporated