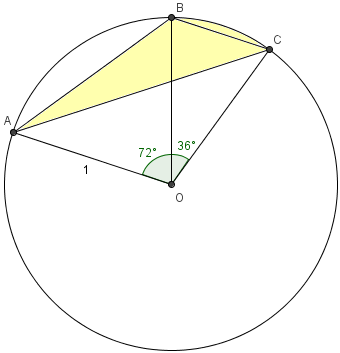
Mock AIME 4 2006-2007 Problems/Problem 4
Problem
Points ![]() ,
, ![]() , and
, and ![]() are on the circumference of a unit circle so that the measure of
are on the circumference of a unit circle so that the measure of ![]() is
is ![]() , the measure of
, the measure of ![]() is
is ![]() , and the measure of
, and the measure of ![]() is
is ![]() . The area of the triangular shape bounded by
. The area of the triangular shape bounded by ![]() and line segments
and line segments ![]() and
and ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution
Let the center of the circle be ![]() . The area of the desired region is easily seen to be that of sector
. The area of the desired region is easily seen to be that of sector ![]() plus the area of triangle
plus the area of triangle ![]() minus the area of triangle
minus the area of triangle ![]() . Using the area formula
. Using the area formula ![]() to compute the areas of the two triangles, this is
to compute the areas of the two triangles, this is ![]() , so the answer is
, so the answer is ![]() .
.
See also
| Mock AIME 4 2006-2007 (Problems, Source) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||