Polya’s method for extremums
Contents
[hide]Polya’s method
People involved in spirituality believe that we are created and placed in the best of all possible worlds.
Therefore, the laws governing our world are based on the principles of optimality.
Natural scientists have found a number of empirical laws and methods that describe nature and therefore optimal laws.
Pólya proposed a method in which the researcher replaces the geometric problem of finding the optimum with a mechanical or optical model and applies empirical dependencies to this model.
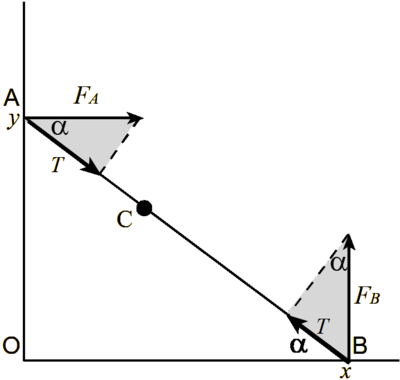
The segment of the shortest length
The segment ![]() has the ends on the sides of a right angle and contains a point
has the ends on the sides of a right angle and contains a point ![]() Find the shortest length of such a segment.
Find the shortest length of such a segment.
Solution
Let's imagine that ![]() is a spring rod that cannot bend, but tends to shorten its length.
is a spring rod that cannot bend, but tends to shorten its length.
The rod is fixed at point ![]() on a hinge without friction. The hinge allows the rod to rotate and slide.
on a hinge without friction. The hinge allows the rod to rotate and slide.
The ends of the rod can slide without friction along the grooves - the sides of the corner.
Let the rod be balanced, and the force pulling it together is equal to ![]() The grooves can create a force only along the normal, so they act on the rod with forces
The grooves can create a force only along the normal, so they act on the rod with forces
![]() For the rod to be balanced, it is required that the moments of the forces be equal relative to point
For the rod to be balanced, it is required that the moments of the forces be equal relative to point ![]() The moments of forces are:
The moments of forces are:
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
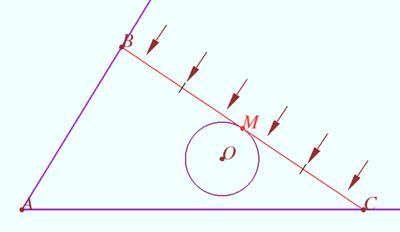
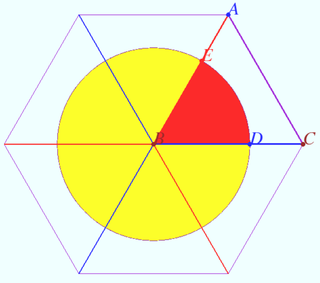
The circle inside a fixed plane angle
Let the plane angle with vertex ![]() and the circle inside the angle be given. A straight line is drawn through point M of this circle, tangent to the circle and intersecting the sides of the angle at points
and the circle inside the angle be given. A straight line is drawn through point M of this circle, tangent to the circle and intersecting the sides of the angle at points ![]() and
and ![]() Find the condition under which the area of
Find the condition under which the area of ![]() is the smallest.
is the smallest.
Solution
Let us imagine that ![]() is a rod that cannot bend, and whose ends slide freely along the sides of the angle, and at point
is a rod that cannot bend, and whose ends slide freely along the sides of the angle, and at point ![]() it rests on a convex curve.
it rests on a convex curve.
Let ![]() be covered with a soap film, which, as usual, tends to reduce its area proportional to the energy.
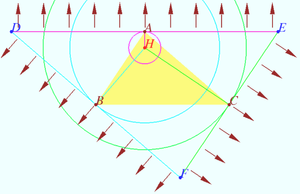
Let ABC be a section of a triangular prism, two faces of which AB and AC are fixed, and the third (BC) is a piston whose width can be changed so that it fits hermetically to the faces AB and AC and can slide along them. The piston rests on a cylinder whose cross-section is a circle with center O.
be covered with a soap film, which, as usual, tends to reduce its area proportional to the energy.
Let ABC be a section of a triangular prism, two faces of which AB and AC are fixed, and the third (BC) is a piston whose width can be changed so that it fits hermetically to the faces AB and AC and can slide along them. The piston rests on a cylinder whose cross-section is a circle with center O.
Air has been removed from the prism. External air presses on the piston and it comes to an equilibrium position. In this case, the energy of the system will be minimal if the volume of the prism becomes minimal.
In the equilibrium position, the moments of forces applied to the piston ![]() on the segments
on the segments ![]() and
and ![]() are equal.
These moments are proportional to the square of the length of the segment, that is, the equilibrium condition is the equality
are equal.
These moments are proportional to the square of the length of the segment, that is, the equilibrium condition is the equality ![]() or
or ![]() is the midpoint
is the midpoint ![]() (the center of mass of a homogeneous segment
(the center of mass of a homogeneous segment ![]() )
)
vladimir.shelomovskii@gmail.com, vvsss
The sphere inside a fixed trihedral angle
There is a sphere inside a fixed trihedral angle with vertex ![]() A plane is drawn through point
A plane is drawn through point ![]() of this sphere, tangent to the sphere and intersecting the edges of the angle at points
of this sphere, tangent to the sphere and intersecting the edges of the angle at points ![]() and
and ![]()
Find the condition under which the volume of the pyramid ![]() is the smallest.
is the smallest.
Solution
Let us imagine the plane ![]() in the form of the piston covering the evacuated volume
in the form of the piston covering the evacuated volume ![]() There is no friction of the piston against the walls.
There is no friction of the piston against the walls.
In the equilibrium position, the volume of the evacuated part of the system is minimal. The equilibrium condition is the equality of the moments of pressure forces, which is equivalent to the equality of the moments of gravity for a homogeneous plate ![]() So the point
So the point ![]() of the contact with the sphere (or any convex solid) must be at the center of mass of the polygon
of the contact with the sphere (or any convex solid) must be at the center of mass of the polygon ![]()
vladimir.shelomovskii@gmail.com, vvsss
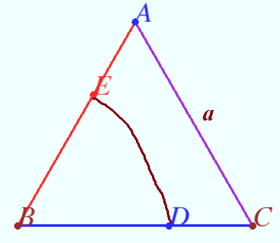
The smallest inscribed equilateral triangle
A right triangle with sides ![]() and
and ![]() be given. Find the area of the smallest regular triangle that can be inscribed in it. All vertices of the required triangle must be located on different sides of this triangle.
be given. Find the area of the smallest regular triangle that can be inscribed in it. All vertices of the required triangle must be located on different sides of this triangle.
Solution
Let's imagine the desired triangle as a cross-section of a drill drilling the plane of a given triangle. The axis of rotation does not have to be in the center of the desired triangle.
Let's turn the drill at a small angle clockwise so that the points of the drill touching the sides of this triangle move along the sides.
The required triangle is minimal, which means that all its vertices cannot lie on its sides. One or more will go inside. When turning counterclockwise the situation is similar.
This means that there is an instantaneous axis of rotation of the drill for such turns. Since the required regular triangle is pedal for a point on the instantaneous axis of rotation, this point is the first Apollonius point of given triangle.
Using the properties of this point, we find that the required area is
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
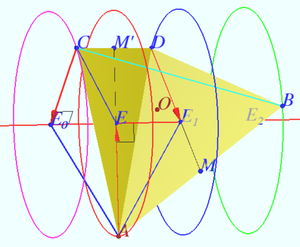
Curve of the smallest length
Find the length of the curve of the smallest length dividing a given equilateral triangle with side ![]() into two equal parts.
into two equal parts.
Solution
Note that the shortest (continuous) curve has ends ![]() and
and ![]() on two sides of the triangle, which we will call blue and red. Let us denote the common vertex of these two sides as
on two sides of the triangle, which we will call blue and red. Let us denote the common vertex of these two sides as ![]()
Let us consider a set of six identical regular triangles in each of which the desired (identical!) curve is drawn.
We place the first of them in an arbitrary way in a certain plane.
We apply the second triangle to the first in the same plane so that the two blue sides and common vertices ![]() of these triangles coincide. In this case, the ends
of these triangles coincide. In this case, the ends ![]() of the curve on the blue line will coincide, that is, the set of these two curves is also a continuous curve.
of the curve on the blue line will coincide, that is, the set of these two curves is also a continuous curve.
We will apply the third triangle to the second so that the red sides, vertices ![]() and points
and points ![]() are coincide. We will similarly apply the fourth, fifth and sixth triangles.
are coincide. We will similarly apply the fourth, fifth and sixth triangles.
As a result, we obtain a regular hexagon formed by sides opposite to vertex ![]() inside which a continuous curve limits an area whose area is equal to half the area of the hexagon. It is equal to the area of the three given triangles.
inside which a continuous curve limits an area whose area is equal to half the area of the hexagon. It is equal to the area of the three given triangles.
It is clear that this is a circle, its area (and radius) are known. The required length of the curve is a sixth of the length of its circumference.
![]()
vladimir.shelomovskii@gmail.com, vvsss
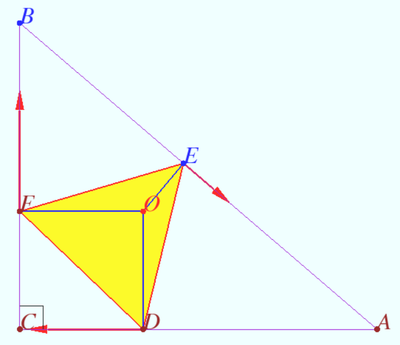
Triangle of the biggest area
A fixed point ![]() in the plane
in the plane ![]() be given. The distances from
be given. The distances from ![]() to the vertices of triangle
to the vertices of triangle ![]() are
are ![]() Find the condition that the area of triangle ABC is maximum.
Find the condition that the area of triangle ABC is maximum.
Solution
Let's imagine that at points ![]() there are rods fixed on hinges that cannot bend or move out of a predetermined plane, but with minimal force they lengthen or shorten. The ends of the rods are connected in pairs in the form of a triangle
there are rods fixed on hinges that cannot bend or move out of a predetermined plane, but with minimal force they lengthen or shorten. The ends of the rods are connected in pairs in the form of a triangle ![]() and slide freely together by changing the length of the rods.
and slide freely together by changing the length of the rods.
Let there be a soap film located in the ![]() plane outside the
plane outside the ![]() triangle, which, as usual, tends to reduce its area proportional to the energy.
triangle, which, as usual, tends to reduce its area proportional to the energy.
The forces applied to the rod ![]() are directed perpendicular to
are directed perpendicular to ![]() therefore
therefore ![]()
In the equilibrium position, the moments of forces applied to the rod ![]() on segments
on segments ![]() and
and ![]() are equal, which means that В is the midpoint of
are equal, which means that В is the midpoint of ![]()
This means that the area ![]() is maximum if
is maximum if ![]() is the center of the circumcircle
is the center of the circumcircle ![]()
The area ![]() is
is ![]() times larger than the area
times larger than the area ![]() respectively, the area
respectively, the area ![]() is maximum if
is maximum if ![]() is the orthocenter of
is the orthocenter of ![]()
vladimir.shelomovskii@gmail.com, vvsss
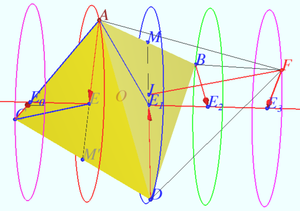
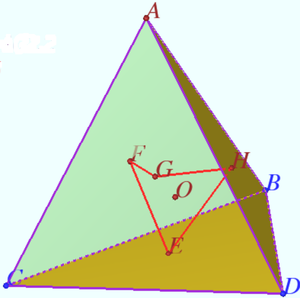
Clever point elephant in hollow tetrahedron
Let the hollow regular unit tetrahedron ![]() be given. A clever point elephant wants to fly along the shortest route that has points belonging to each face of the tetrahedron.
be given. A clever point elephant wants to fly along the shortest route that has points belonging to each face of the tetrahedron.
Find the length of this path.
Solution
Denote ![]()
Let ![]() and
and ![]() be the medians of the faces
be the medians of the faces ![]() and
and ![]()
Let ![]()
It is known that the common perpendicular to these medians is ![]()
1. Note that ![]()
Let ![]() be symmetrical to
be symmetrical to ![]() with respect to
with respect to ![]()
Then ![]()
We similarly prove that ![]()
This means that all the vertices of the tetrahedron are located on circles of equal radius with centers on straight line ![]() and the distances between the centers of the circles are equal.
and the distances between the centers of the circles are equal.
Consequently, the tetrahedron is inscribed in a cylinder ![]() of radius
of radius ![]() with axis
with axis ![]()
2. Let ![]() be the angle between
be the angle between ![]() and
and ![]()
![]()
![]() Let
Let ![]() be the center of the
be the center of the ![]() face,
face, ![]()
Let point ![]() be symmetrical to
be symmetrical to ![]() with respect to
with respect to ![]() is symmetrical to
is symmetrical to ![]() with respect to
with respect to ![]()
![]() is located in the plane containing
is located in the plane containing ![]() perpendicular to the straight line
perpendicular to the straight line ![]() that is, this point lies on
that is, this point lies on ![]() and the tetrahedron
and the tetrahedron ![]()
Similarly, we will construct an arbitrarily long chain of equal tetrahedra inscribed in a cylinder whose median faces contain a sequence of points ![]()
It follows that the shortest path of the elephant cannot be shorter than ![]() There are some such ways inside the tetrahedron. One of them is shown in the diagram.
There are some such ways inside the tetrahedron. One of them is shown in the diagram.
vladimir.shelomovskii@gmail.com, vvsss