Radical axis
Contents
[hide]Introduction
The theory of radical axis is a priceless geometric tool that can solve formidable geometric problems fairly readily. Problems involving it can be found on many major math olympiad competitions, including the prestigious USAMO. Therefore, any aspiring math olympian should peruse this material carefully, as it may contain the keys to one's future success.
Not all theorems will be fully proven in this text. The objective of this document is to introduce you to some key concepts, and then give you a chance to derive some of the beautiful results on your own. In that way, you will understand and retain the information in here much more solidly. Finally, your newfound knowledge will be tested on a few challenging problems that are exemplary examples on how radical axis theory can be used and why it pertains to that situation. I hope after you read this text, you will become a better math student, armed with another tool to solve difficult problems. But, anyway, good luck. i
Definitions
The power of point ![]() with respect to circle
with respect to circle ![]() (with radius
(with radius ![]() and center
and center ![]() ), which shall thereafter be dubbed
), which shall thereafter be dubbed ![]() , is defined to equal
, is defined to equal ![]() .
.
Note that the power of a point is negative if the point is inside the circle.
The radical axis of two non-concentric circles ![]() is defined as the locus of the points
is defined as the locus of the points ![]() such that the power of
such that the power of ![]() with respect to
with respect to ![]() and
and ![]() are equal. In other words, if
are equal. In other words, if ![]() are the center and radius of
are the center and radius of ![]() , then a point
, then a point ![]() is on the radical axis if and only if
is on the radical axis if and only if ![]() (i.e., the radical axis is the line that one gets when you subtract the equations of two circles).
(i.e., the radical axis is the line that one gets when you subtract the equations of two circles).
Results
Theorem 1: (Power of a Point)
If a line drawn through point P intersects circle ![]() at points A and B, then
at points A and B, then ![]() .
.
Theorem 2: (Radical Axis Theorem)
a. The radical axis is a line perpendicular to the line connecting the circles' centers (line ![]() ).
).
b. If the two circles intersect at two common points, their radical axis is the line through these two points.
c. If they intersect at one point, their radical axis is the common internal tangent.
d. If the circles do not intersect, and if one does not fully contain the other, their radical axis is the perpendicular to ![]() through point A, the unique point on
through point A, the unique point on ![]() such that
such that ![]() .
.
Theorem 3: (Radical Axis Concurrence Theorem) The three pairwise radical axes of three circles concur at a point, called the radical center.
Theorem 4: (Radical Centre of Intersecting Circles) (EGMO Theorem 2.9)
Let ![]() and
and ![]() be two circles with centers
be two circles with centers ![]() and
and ![]() . Select two points A and B on
. Select two points A and B on ![]() and C and D on
and C and D on ![]() . Then the following are equivalent
. Then the following are equivalent
 lie on a circle with center
lie on a circle with center  not on line
not on line  .
.- Lines
 and
and  intersect on the radical axis of
intersect on the radical axis of  and
and  .
.
Theorem 5: (EGMO Lemma 2.11)
Let ABC be a triangle and consider a point ![]() in its interior. Suppose that
in its interior. Suppose that ![]() is tangent to
is tangent to ![]() and
and ![]() , ray
, ray ![]() bisects
bisects ![]()
Proofs
Theorem 1 is trivial Power of a Point, and thus is left to the reader as an exercise. (Hint: Draw a line through P and the center.)
Theorem 2 shall be proved here. Assume the circles are ![]() and
and ![]() with centers
with centers ![]() and
and ![]() and radii
and radii ![]() and
and ![]() , respectively. (It may be a good idea for you to draw some circles here.)
, respectively. (It may be a good idea for you to draw some circles here.)
First, we tackle part (b). Suppose the circles intersect at points ![]() and
and ![]() and point P lies on
and point P lies on ![]() . Then by Theorem 1 the powers of P with respect to both circles are equal to
. Then by Theorem 1 the powers of P with respect to both circles are equal to ![]() , and hence by transitive
, and hence by transitive ![]() . Thus, if point P lies on
. Thus, if point P lies on ![]() , then the powers of P with respect to both circles are equal.
, then the powers of P with respect to both circles are equal.
Now, we prove the inverse of the statement just proved; because the inverse is equivalent to the converse, the if and only if would then be proven. Suppose that P does not lie on ![]() . In particular, line
. In particular, line ![]() does not intersect X. Then
does not intersect X. Then ![]() intersects circles
intersects circles ![]() and
and ![]() a second time at distinct points
a second time at distinct points ![]() and
and ![]() , respectively. (If
, respectively. (If ![]() is tangent to
is tangent to ![]() , for example, we adopt the convention that
, for example, we adopt the convention that ![]() ; similar conventions hold for
; similar conventions hold for ![]() . Power of a Point still holds in this case. Also, notice that
. Power of a Point still holds in this case. Also, notice that ![]() and
and ![]() cannot both equal
cannot both equal ![]() , as
, as ![]() cannot be tangent to both circles.) Because
cannot be tangent to both circles.) Because ![]() is not equal to
is not equal to ![]() , so
, so ![]() does not equal
does not equal ![]() , and thus by Theorem 1
, and thus by Theorem 1 ![]() is not congruent to
is not congruent to ![]() , as desired. This completes part (b).
, as desired. This completes part (b).
For the remaining parts, we employ a lemma:
Lemma 1: Let ![]() be a point in the plane, and let
be a point in the plane, and let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() . Then
. Then ![]() .
.
The proof of the lemma is an easy application of the Pythagorean Theorem and will again be left to the reader as an exercise.
Lemma 2: There is an unique point P on line ![]() such that
such that ![]() .
.
Proof: First show that P lies between ![]() and
and ![]() via proof by contradiction, by using a bit of inequality theory and the fact that
via proof by contradiction, by using a bit of inequality theory and the fact that ![]() . Then, use the fact that
. Then, use the fact that ![]() (a constant) to prove the lemma.
(a constant) to prove the lemma.
Lemma 1 shows that every point on the plane can be equivalently mapped to a line on ![]() . Lemma 2 shows that only one point in this mapping satisfies the given condition. Combining these two lemmas shows that the radical axis is a line perpendicular to
. Lemma 2 shows that only one point in this mapping satisfies the given condition. Combining these two lemmas shows that the radical axis is a line perpendicular to ![]() , completing part (a).
, completing part (a).
Parts (c) and (d) will be left to the reader as an exercise. (Also, try proving part (b) solely using the lemmas.)
Now, try to prove Theorem 3 on your own! (Hint: Let P be the intersection of two of the radical axes.)The proof of this theorem along with the proof of Theorem 4are given in EGMO as Example 2.7 and Theorem 2.9.
Theorem 5
Let ![]() intersect at
intersect at ![]() at
at ![]() and let
and let ![]() ,
, ![]() . Clearly,
. Clearly, ![]() is a radical axis of
is a radical axis of ![]() ,
, ![]() . We see that
. We see that![]() as desired.
as desired.
Exercises
If you haven't already done so, prove the theorems and lemmas outlined in the proofs section. Note: No solutions will be provided to the following problems(laziness). If you are stuck, ask on the forum.
Problem 1. Two circles ![]() and
and ![]() intersect at
intersect at ![]() and
and ![]() . Point
. Point ![]() is located on
is located on ![]() such that
such that ![]() and
and ![]()
15 ![]() . If the radius of
. If the radius of ![]() is
is ![]() , find the radius of
, find the radius of ![]() . Note: An error in this problem previously rendered it unsolvable.
. Note: An error in this problem previously rendered it unsolvable.
Problem 2. Solve 2009 USAMO Problem 1. If you already know how to solve it.
Problem 3. Two circles P and Q with radii 1 and 2, respectively, intersect at X and Y. Circle P is to the left of circle Q. Prove that point A is to the left of ![]() if and only if
if and only if ![]() .
.
Problem 4. Solve 2012 USAJMO Problem 1.
Problem 5. Does Theorem 2 apply to circles in which one is contained inside the other? How about internally tangent circles? Concentric circles?
Problem 6. Construct the radical axis of two circles. What happens if one circle encloses the other?
Problem 7. Solve 1995 IMO Problem 1 in two different ways. Compare your solutions with the solutions provided.
Problems
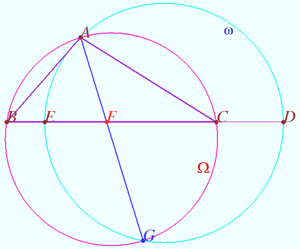
Simple
Let triangle ![]() points
points ![]() and
and ![]() be given. Denote
be given. Denote
![]()
![]()
Prove that ![]()
Proof
WLOG, the order of the points is ![]() as shown on diagram.
as shown on diagram.
![]()
![]()
![]()
![]()
Intermediate
2021 AIME Problem 13. Circles ![]() and
and ![]() with radii
with radii ![]() and
and ![]() , respectively, intersect at distinct points
, respectively, intersect at distinct points ![]() and
and ![]() . A third circle
. A third circle ![]() is externally tangent to both
is externally tangent to both ![]() and
and ![]() . Suppose line
. Suppose line ![]() intersects
intersects ![]() at two points
at two points ![]() and
and ![]() such that the measure of minor arc
such that the measure of minor arc ![]() is
is ![]() . Find the distance between the centers of
. Find the distance between the centers of ![]() and
and ![]() .
.
Olympiad
2014 USAMO Problem 5. Let ![]() be a triangle with orthocenter
be a triangle with orthocenter ![]() and let
and let ![]() be the second intersection of the circumcircle of triangle
be the second intersection of the circumcircle of triangle ![]() with the internal bisector of the angle
with the internal bisector of the angle ![]() . Let
. Let ![]() be the circumcenter of triangle
be the circumcenter of triangle ![]() and
and ![]() the orthocenter of triangle
the orthocenter of triangle ![]() . Prove that the length of segment
. Prove that the length of segment ![]() is equal to the circumradius of triangle
is equal to the circumradius of triangle ![]() .
.
2017 USAMO Problem 3. Let ![]() be a scalene triangle with circumcircle
be a scalene triangle with circumcircle ![]() and incenter
and incenter ![]() Ray
Ray ![]() meets
meets ![]() at
at ![]() and
and ![]() again at
again at ![]() the circle with diameter
the circle with diameter ![]() cuts
cuts ![]() again at
again at ![]() Lines
Lines ![]() and
and ![]() meet at
meet at ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() The circumcircles of
The circumcircles of ![]() and
and ![]() intersect at points
intersect at points ![]() and
and ![]() Prove that
Prove that ![]() passes through the midpoint of either
passes through the midpoint of either ![]() or
or ![]()
2012 IMO Problem 5. Let ![]() be a triangle with
be a triangle with ![]() , and let
, and let ![]() be the foot of the altitude from
be the foot of the altitude from ![]() . Let
. Let ![]() be a point in the interior of the segment
be a point in the interior of the segment ![]() . Let
. Let ![]() be the point on the segment
be the point on the segment ![]() such that
such that ![]() . Similarly, let
. Similarly, let ![]() be the point on the segment
be the point on the segment ![]() such that
such that ![]() . Let
. Let ![]() . Prove that
. Prove that ![]() .
.
See Also
This article is a stub. Help us out by expanding it.