Symmetry
A proof utilizes symmetry if the steps to prove one thing is identical to those steps of another. For example, to prove that in triangle ABC with all three sides congruent to each other that all three angles are equal, you only need to prove that if ![]() then
then ![]() the other cases hold by symmetry because the steps are the same.
the other cases hold by symmetry because the steps are the same.
Contents
[hide]- 1 Hidden symmetry
- 2 Symmetry with respect angle bisectors
- 3 Symmetry with respect angle bisectors 1
- 4 Construction of triangle
- 5 Symmetry with respect angle bisectors 2
- 6 Symmetry of radical axes
- 7 Composition of symmetries
- 8 Composition of symmetries 1
- 9 Composition of symmetries 2
- 10 Symmetry and secant
- 11 Symmetry and incircle
- 12 Symmetry and incircle A
- 13 Symmetry for 60 degrees angle
- 14 See also
Hidden symmetry
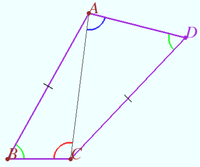
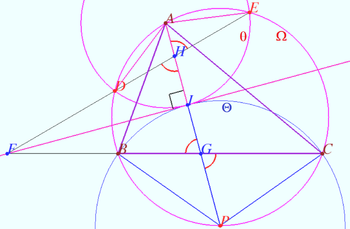
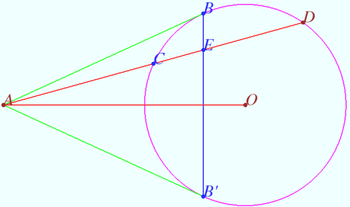
Let the convex quadrilateral ![]() be given.
be given.
![]()
Prove that ![]()
Proof
Let ![]() be bisector
be bisector ![]()
Let point ![]() be symmetric
be symmetric ![]() with respect
with respect ![]()
![]()
![]() is isosceles.
is isosceles.
Therefore ![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
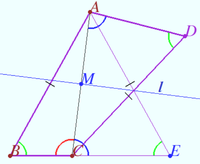
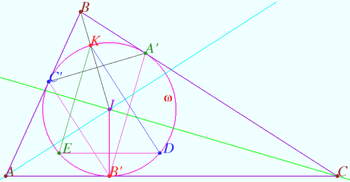
Symmetry with respect angle bisectors
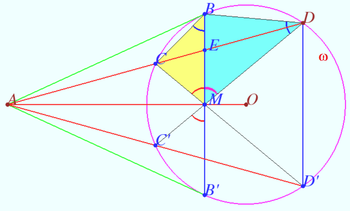
Given the triangle ![]() is the incircle,
is the incircle, ![]() is the incenter,
is the incenter, ![]()
Points ![]() and
and ![]() are symmetrical to point
are symmetrical to point ![]() with respect to the lines containing the bisectors
with respect to the lines containing the bisectors ![]() and
and ![]() respectively.
respectively.
Prove that ![]() is the midpoint
is the midpoint ![]()
Proof
![]() Denote
Denote ![]()
The tangents from point ![]() to
to ![]() are equal
are equal ![]()
Point ![]() is symmetrical to point
is symmetrical to point ![]() with respect
with respect ![]() is symmetrical to segment
is symmetrical to segment ![]()
Symilarly, ![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Symmetry with respect angle bisectors 1
The bisector ![]() intersect the incircle
intersect the incircle ![]() of the triangle
of the triangle ![]() at the point
at the point ![]() The point
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() the point
the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() Prove that
Prove that ![]() is the bisector of the segment
is the bisector of the segment ![]()
Proof
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
Similarly ![]()
vladimir.shelomovskii@gmail.com, vvsss
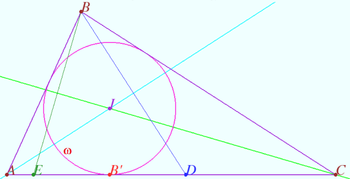
Construction of triangle
Given points ![]() and
and ![]() at which the segments of the bisectors
at which the segments of the bisectors ![]() and
and ![]() respectively intersect the incircle of
respectively intersect the incircle of ![]() centered at
centered at ![]()
Construct the triangle ![]()
Construction
We construct the incenter of ![]() as circumcenter of
as circumcenter of ![]()
If these points are collinear or if ![]() construction is impossible.
construction is impossible.
We construct bisectors ![]() and
and ![]()
We construct the points ![]() and
and ![]() symmetrical to point
symmetrical to point ![]() with respect to
with respect to ![]() and
and ![]() respectively.
respectively.
We construct the bisector ![]() and choose the point
and choose the point ![]() as the point intersection with the circle
as the point intersection with the circle ![]() closest to the line
closest to the line ![]()
We construct a tangent to the the circle ![]() at the point
at the point ![]() It intersects the lines
It intersects the lines ![]() and
and ![]() at points
at points ![]() and
and ![]() respectively.
respectively.
We construct the tangents to ![]() which are symmetrical to sideline
which are symmetrical to sideline ![]() with respect to
with respect to ![]() and
and ![]()
vladimir.shelomovskii@gmail.com, vvsss
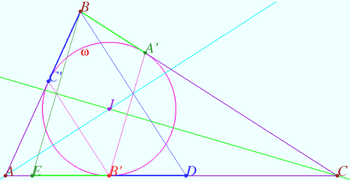
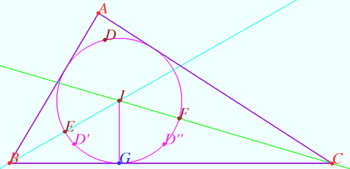
Symmetry with respect angle bisectors 2
Given the triangle ![]() is the incircle,
is the incircle, ![]() is the incenter,
is the incenter,
![]()
Let ![]() be the point on sideline
be the point on sideline ![]()
Points ![]() and
and ![]() are symmetrical to point
are symmetrical to point ![]() with respect to the lines
with respect to the lines ![]() and
and ![]() respectively. The line
respectively. The line ![]() contains point
contains point ![]()
Prove that ![]() is the midpoint
is the midpoint ![]()
Proof
The segment ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() the segment
the segment ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() So
So ![]()
Similarly ![]() at midpoint
at midpoint ![]()
![]()
![]() or
or ![]()
![]()
![]() or
or ![]()
![]() We use the Law of Sines and get:
We use the Law of Sines and get:
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Symmetry of radical axes
Let triangle ![]() be given. The point
be given. The point ![]() and the circle
and the circle ![]() are the incenter and the circumcircle of
are the incenter and the circumcircle of ![]()
Circle ![]() centered at
centered at ![]() has the radius
has the radius ![]() and intersects
and intersects ![]() at points
at points ![]() and
and ![]() Line
Line ![]() is the tangent for
is the tangent for ![]() at the point
at the point ![]()
Prove that line ![]() is symmetry to the line
is symmetry to the line ![]() with respect axis
with respect axis ![]()
Proof
![]() circle
circle ![]() centered at
centered at ![]() contain points
contain points ![]() and
and ![]() and is tangent for
and is tangent for ![]() and
and ![]()
![]() is the radical axis of
is the radical axis of ![]() and
and ![]()
![]() is the radical axis of
is the radical axis of ![]() and
and ![]()
![]() is the radical axis of
is the radical axis of ![]() and
and ![]() and
and ![]() are concurrent (at point
are concurrent (at point ![]() )
)
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
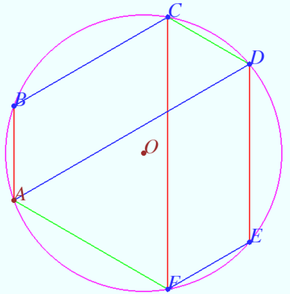
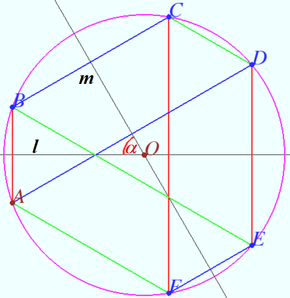
Composition of symmetries
Let the inscribed convex hexagon ![]() be given,
be given,
![]() Prove that
Prove that ![]()
Proof
Denote ![]() the circumcenter of
the circumcenter of ![]()
![]() the common bisector
the common bisector ![]() the common bisector
the common bisector ![]()
![]() the smaller angle between lines
the smaller angle between lines ![]() and
and ![]()
![]() is the symmetry with respect axis
is the symmetry with respect axis ![]() is the symmetry with respect axis
is the symmetry with respect axis ![]()
It is known that the composition of two axial symmetries with non-parallel axes is a rotation centered at point of intersection of the axes at twice the angle from the axis of the first symmetry to the axis of the second symmetry.
![]()
![]()
![]() Therefore
Therefore ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
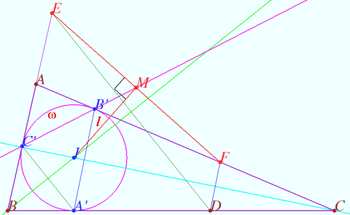
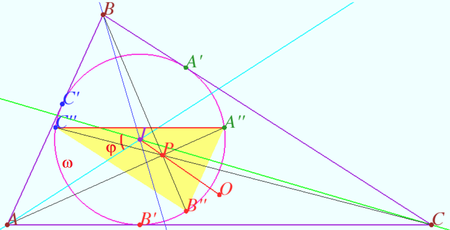
Composition of symmetries 1
Let the triangle ![]() be given.
be given.
![]() is the incircle,
is the incircle, ![]() is the incenter,
is the incenter, ![]() is the circumcenter of
is the circumcenter of ![]()
![]() The point
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
Prove: a)![]()
b) ![]()
Proof
a) Denote ![]() the smaller angle between
the smaller angle between ![]() and
and ![]()
![]() is the symmetry with respect axis
is the symmetry with respect axis ![]() is the symmetry with respect axis
is the symmetry with respect axis ![]()
![]() counterclockwise direction.
counterclockwise direction.
![]() clockwise direction.
clockwise direction.
Therefore ![]() is parallel to tangent line for
is parallel to tangent line for ![]() at point
at point ![]()
b) ![]() is homothetic to
is homothetic to ![]()
![]() is the circumcenter of
is the circumcenter of ![]()
The center of the homothety lies on the line passing through the circumcenters of the triangles. ![]()
vladimir.shelomovskii@gmail.com, vvsss
Composition of symmetries 2
Let triangle ![]() be given. The point
be given. The point ![]() and the circle
and the circle ![]() are the incenter and the incircle of
are the incenter and the incircle of ![]()
Let ![]() be the symmetry with respect axis
be the symmetry with respect axis ![]() be the symmetry with respect axis
be the symmetry with respect axis ![]() the symmetry with respect axis
the symmetry with respect axis ![]()
![]() Find the composition of axial symmetries with respect
Find the composition of axial symmetries with respect ![]() and
and ![]()
Solution
It is known that the composition of three axial symmetries whose axes intersect at one point ![]() is an axial symmetry whose axis contains the same point
is an axial symmetry whose axis contains the same point ![]()
Consider the composition of axial symmetries for point ![]()
![]() is a fixed point of transformation.
is a fixed point of transformation.
This means that the desired axis of symmetry contains points ![]() and
and ![]() , this is a straight line
, this is a straight line ![]()
vladimir.shelomovskii@gmail.com, vvsss
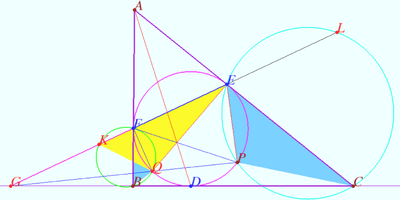
Symmetry and secant
The circle ![]() centered at
centered at ![]() and the point
and the point ![]() be given. Let
be given. Let ![]() and
and ![]() be the tangents,
be the tangents, ![]() be the secant (
be the secant (![]()
Segment ![]() intersects segment
intersects segment ![]() at point
at point ![]() Prove that
Prove that ![]()
Proof
Let ![]() be symmetric to
be symmetric to ![]() with respect the line
with respect the line ![]()
![]()
It is known that ![]()
![]() We use symmetry and get
We use symmetry and get ![]() It is known that
It is known that ![]()
![]()
Triangles ![]() and
and ![]() have common side
have common side ![]()
Similar triangles ![]() and
and ![]() have the areas ratio
have the areas ratio ![]()
Therefore ![]()
According the Cross-ratio criterion the four points ![]() are a harmonic range (on the real projective line).
are a harmonic range (on the real projective line).
vladimir.shelomovskii@gmail.com, vvsss
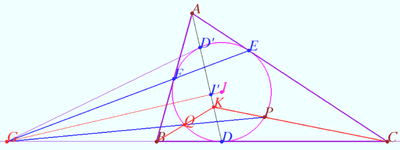
Symmetry and incircle
Let ![]() with incircle
with incircle ![]() be given.
be given.
Point ![]()
1. Let ![]() be the point in
be the point in ![]()
Denote ![]()
Prove that ![]()
2. Let ![]() be the point in the segment
be the point in the segment ![]()
Let ![]() be the point in the ray
be the point in the ray ![]() such that
such that ![]()
Denote ![]()
Prove that points ![]() and
and ![]() are collinear.
are collinear.
Proof
![]()
![]() We use Menelaus theorem for a triangle
We use Menelaus theorem for a triangle ![]() and a transversal line
and a transversal line ![]() and get:
and get:
![]()
![]()
![]()
![]()
2. Denote ![]() Then
Then
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Symmetry and incircle A
Denote ![]() is the arbitrary point.
is the arbitrary point. ![]()
Prove that ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Denote ![]() is the incenter of
is the incenter of ![]()
Let us make the projective transformations mapping circle ![]() onto circle and point
onto circle and point ![]() onto center of this circle.
onto center of this circle.
Denote ![]() the result of transformation
the result of transformation ![]() of point
of point ![]() This transformation maps point
This transformation maps point ![]() to infinity.
to infinity.
Segment ![]() this transformation maps onto diameter
this transformation maps onto diameter ![]() onto
onto ![]()
We use the cross-ratio ![]() which is fixed, equation
which is fixed, equation ![]() the Claim, and get
the Claim, and get
![]() so
so ![]() is the midpoint of
is the midpoint of ![]()
Point ![]() in infinity, so
in infinity, so ![]()
Lines ![]() and
and ![]() are crossing at the line of symmetry
are crossing at the line of symmetry ![]() therefore lines
therefore lines ![]() and
and ![]() are concurrent.
are concurrent.
Claim
Let ![]() with incircle
with incircle ![]() be given.
be given.
Point ![]() Prove
Prove ![]()
Proof
WLOG, ![]() Denote
Denote ![]() the point in
the point in ![]() such that
such that ![]()
![]()
![]() Denote
Denote ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
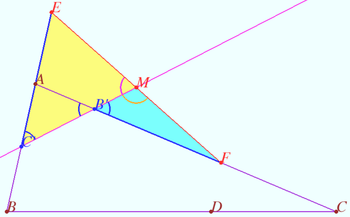
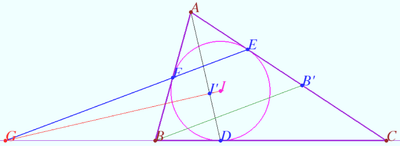
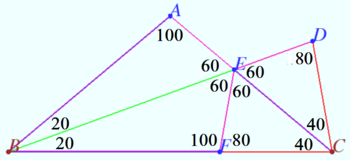
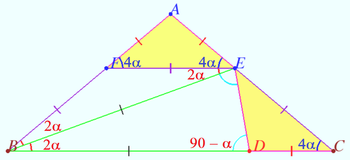
Symmetry for 60 degrees angle
Let an isosceles triangle ![]() be given.
be given.
Let ![]() be the bisector of
be the bisector of ![]()
a) ![]() Prove that
Prove that ![]()
b) ![]() Prove that
Prove that ![]()
Proof
a) One can find successively angles (see diagram).
b) Let ![]()
Let ![]()
Let ![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss