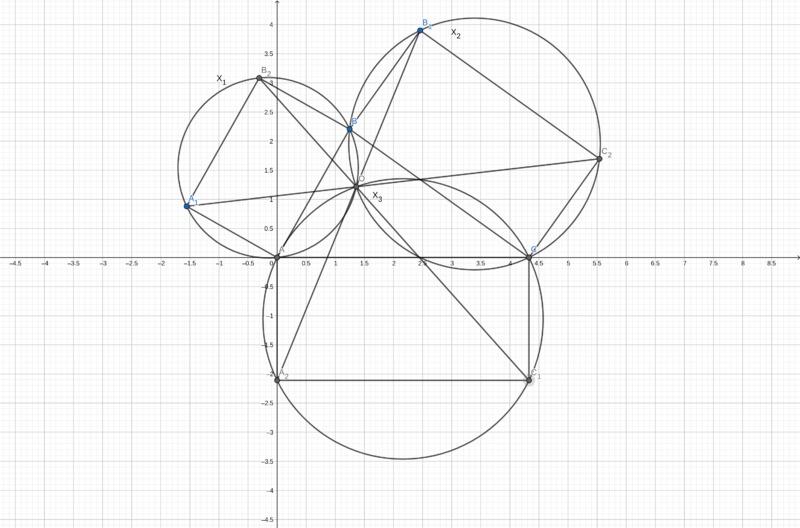
Talk:2021 USAMO Problems/Problem 1
We are given the acute triangle ![]() , rectangles
, rectangles ![]() such that
such that ![]() . Let's call
. Let's call ![]() .
.
Construct circumcircles ![]() around the rectangles
around the rectangles ![]() respectively.
respectively. ![]() intersect at two points:
intersect at two points: ![]() and a second point we will label
and a second point we will label ![]() . Now
. Now ![]() is a diameter of
is a diameter of ![]() , and
, and ![]() is a diameter of
is a diameter of ![]() , so
, so ![]() , and
, and ![]() , so
, so ![]() is on the diagonal
is on the diagonal ![]() .
.
![]() (angles standing on the same arc of the circle
(angles standing on the same arc of the circle ![]() ), and similarly,
), and similarly, ![]() . Therefore,
. Therefore, ![]() .
.
Construct another circumcircle ![]() around the triangle
around the triangle ![]() , which intersects
, which intersects ![]() in
in ![]() , and
, and ![]() in
in ![]() . We will prove that
. We will prove that ![]() . Note that
. Note that ![]() is a cyclic quadrilateral in
is a cyclic quadrilateral in ![]() , so since
, so since ![]() ,
, ![]() is a diameter of
is a diameter of ![]() and
and ![]() - so
- so ![]() is a rectangle.
is a rectangle.
Since ![]() ,
, ![]() is a diameter of
is a diameter of ![]() , and
, and ![]() . Similarly,
. Similarly, ![]() , so O is on
, so O is on ![]() , and by opposite angles,
, and by opposite angles, ![]() .
.
Finally, since ![]() is on
is on ![]() and
and ![]() is on
is on ![]() , that gives
, that gives ![]() - meaning
- meaning ![]() is on the line
is on the line ![]() . But
. But ![]() is also on the line
is also on the line ![]() - so
- so ![]() . Similarly,
. Similarly, ![]() . So the three diagonals
. So the three diagonals ![]() intersect in
intersect in ![]() .
.