2024 AMC 12B Problems/Problem 12

Problem

Let $z$ be a complex number with real part greater than $1$ and $|z|=2$ . In the complex plane, the four points $0$ , $z$ , $z^2$ , and $z^3$ are the vertices of a quadrilateral with area $15$ . What is the imaginary part of $z$ ?

$\textbf{(A) }\frac{3}{4}\qquad\textbf{(B) }1\qquad\textbf{(C) }\frac{4}{3}\qquad\textbf{(D) }\frac{3}{2}\qquad\textbf{(E) }\frac{5}{3}$

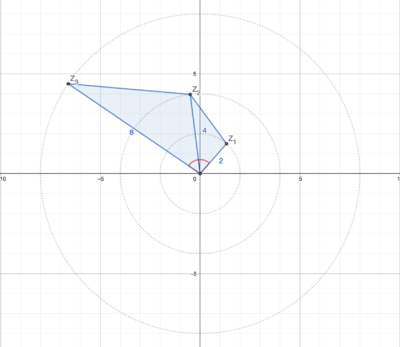
Diagram

Solution 1 (similar triangles)

By making a rough estimate of where $z$ , $z^2$ , and $z^3$ are on the complex plane, we can draw a pretty accurate diagram (like above.)

Here, points $Z_1$ , $Z_2$ , and $Z_3$ lie at the coordinates of $z$ , $z^2$ , and $z^3$ respectively, and $O$ is the origin.

We're given $|z|=2$ , so $|z^2|=|z|^2=4$ and $|z^3|=|z|^3 = 8$ . This gives us $OZ_1=2$ , $OZ_2=4$ , and $OZ_3=8$ .

Additionally, we know that $\angle{Z_1OZ_2}\cong\angle{Z_2OZ_3}$ (since every power of $z$ rotates around the origin by the same angle.) We set these angles equal to $\theta$ .

This gives us enough info to say that $\triangle{OZ_1Z_2}\sim\triangle{OZ_2Z_3}$ by SAS similarity (since $\frac{OZ_2}{OZ_1}=\frac{OZ_3}{OZ_2}=2$ .)

It follows that $[OZ_1Z_2Z_3]=[OZ_1Z_2]+[OZ_2Z_3]=[OZ_1Z_2]+2^2[OZ_1Z_2]=5[OZ_1Z_2]$ as the ratio of side lengths of the two triangles is 2 to 1.

This means $5[OZ_1Z_2]=15$ or $[OZ_1Z_2]=3$ as we were given $[OZ_1Z_2Z_3]=15$ .

Using $A=\frac{a*b*sinC}{2}$ , we get that $[OZ_1Z_2]=\frac{2*4*sin(\theta)}{2}=4sin(\theta)$ , so $4sin(\theta)=3$ , giving $sin(\theta)=\frac{3}{4}$ .

Thus, $Im(z)=|z|sin(\theta)=2(\frac{3}{4})=\boxed{\textbf{(D) }\frac{3}{2}}$ .

~nm1728

Solution 2 (shoelace theorem)

We have the vertices:

1. $0$ at $(0, 0)$

2. $z$ at $(2\cos \theta, 2\sin \theta)$

3. $z^2$ at $(4\cos 2\theta, 4\sin 2\theta)$

4. $z^3$ at $(8\cos 3\theta, 8\sin 3\theta)$

The Shoelace formula for the area is: $\text{Area} = \frac{1}{2} \left| x_1 y_2 + x_2 y_3 + x_3 y_4 + x_4 y_1 - (y_1 x_2 + y_2 x_3 + y_3 x_4 + y_4 x_1) \right|.$ $\text{Area} = \frac{1}{2} \left| 0 + 2\cos \theta \cdot 4\sin 2\theta + 4\cos 2\theta \cdot 8\sin 3\theta - (2\sin \theta \cdot 4\cos 2\theta + 4\sin 2\theta \cdot 8\cos 3\theta) \right|.$ $\text{Area} = \frac{1}{2} \left| 8\cos \theta \sin 2\theta + 32\cos 2\theta \sin 3\theta - 8\sin \theta \cos 2\theta - 32\sin 2\theta \cos 3\theta \right|.$ $\text{Area} = \frac{1}{2} \left|8\cos \theta \sin 2\theta - 8\sin \theta \cos 2\theta) + (32\cos 2\theta \sin 3\theta - 32\sin 2\theta \cos 3\theta)) \right|.$ $\text{Area} = \frac{1}{2} \left|8\sin(2\theta - \theta) + (32\sin(2\theta - \theta) \right|.$

Given that the area is 15: $\frac{1}{2} \left| 40\sin \theta \right| = 15.$ $20|\sin \theta| = 15 \implies |\sin \theta| = \frac{3}{4}.$ Since $\theta$ corresponds to a complex number $z$ with a positive imaginary part, we have:

$\sin \theta = \frac{3}{4}.$ $\text{Imaginary part} = 2\sin \theta = 2 \times \frac{3}{4} = \boxed{\textbf{(D) }\frac{3}{2}}.$

~luckuso

2024 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 11	Followed by Problem 13
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search

2024 AMC 12B Problems/Problem 12

Contents

Problem

Diagram

Solution 1 (similar triangles)

Solution 2 (shoelace theorem)

See also