Difference between revisions of "2005 PMWC Problems/Problem T8"
m (→Solution) |
m (→Problem) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
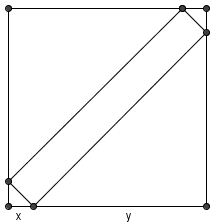
| − | An [[isosceles triangle|isosceles]] [[right triangle]] is removed from each corner of a [[square]] piece of paper so that a [[rectangle]] of unequal sides remains. If the sum of the areas of the cut-off pieces is | + | An [[isosceles triangle|isosceles]] [[right triangle]] is removed from each corner of a [[square]] piece of paper so that a [[rectangle]] of unequal sides remains. If the sum of the areas of the cut-off pieces is <math>200</math> and the lengths of the legs of the triangles cut off are integers, find the area of the rectangle. |
== Solution == | == Solution == | ||
Revision as of 11:04, 24 December 2019
Problem
An isosceles right triangle is removed from each corner of a square piece of paper so that a rectangle of unequal sides remains. If the sum of the areas of the cut-off pieces is 
and the lengths of the legs of the triangles cut off are integers, find the area of the rectangle.
Solution
Since the figure in the middle is a rectangle, the isosceles triangles on opposite vertices are congruent. Let 
be a leg of the first two, and 
the other two. The sum of the areas of the triangle is then 
. (Remember that the sides are of unequal lengths, so we exclude 
). Since squares 
, we can reduce our search to even integers, and a short bit of trial and error yield 
works.
Using subtraction of areas or 45-45-90 triangles, we find that the area of the rectangle is 
; so the area of the rectangle is 
.
See also
| 2005 PMWC (Problems) | ||
| Preceded by Problem T7 |
Followed by Problem T9 | |
| I: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 T: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 | ||
