Difference between revisions of "2021 USAJMO Problems/Problem 2"
| Line 1: | Line 1: | ||
| + | ==Problem== | ||
Rectangles <math>BCC_1B_2,</math> <math>CAA_1C_2,</math> and <math>ABB_1A_2</math> are erected outside an acute triangle <math>ABC.</math> Suppose that<cmath>\angle BC_1C+\angle CA_1A+\angle AB_1B=180^{\circ}.</cmath>Prove that lines <math>B_1C_2,</math> <math>C_1A_2,</math> and <math>A_1B_2</math> are concurrent. | Rectangles <math>BCC_1B_2,</math> <math>CAA_1C_2,</math> and <math>ABB_1A_2</math> are erected outside an acute triangle <math>ABC.</math> Suppose that<cmath>\angle BC_1C+\angle CA_1A+\angle AB_1B=180^{\circ}.</cmath>Prove that lines <math>B_1C_2,</math> <math>C_1A_2,</math> and <math>A_1B_2</math> are concurrent. | ||
| + | |||
| + | ==Solution== | ||
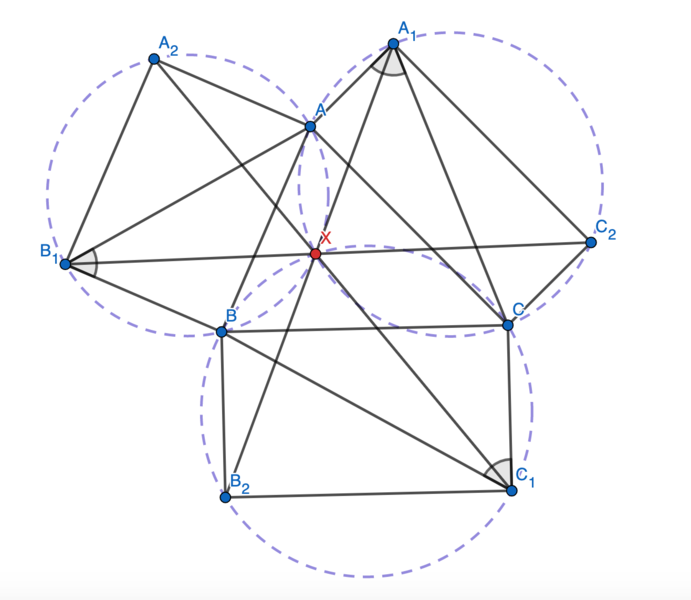
| + | [[Image:Leonard my dude.png|frame|none|###px|]] | ||
| + | |||
| + | We first claim that the three circles <math>(BCC_1B_2),</math> <math>(CAA_1C_2),</math> and <math>(ABB_1A_2)</math> are share a common intersection. | ||
| + | |||
| + | Let the second intersection of <math>(BCC_1B_2)</math> and <math>(CAA_1C_2)</math> be <math>K</math>. Then | ||
| + | <cmath>\begin{align*} | ||
| + | \angle AKC &= 360^\circ - \angle BKA - \angle CKB \ | ||
| + | &= 360^\circ - (180^\circ - \angle AB_1B + 180^\circ - \angle BC_1C) \& | ||
| + | = 180^\circ - \angle CA_1A, | ||
| + | \end{align*}</cmath> | ||
| + | which implies that <math>AA_1C_2CK</math> is cyclic as desired. | ||
| + | |||
| + | Now we show that <math>K</math> is the intersection of <math>B_1C_2,</math> <math>C_1A_2,</math> and <math>A_1B_2.</math> Note that <math>\angle C_1XB = \angle BXA_2 = 90^\circ,</math> so <math>A_2, K, C_1</math> are collinear. Similarly, <math>B_1, K, C_2</math> and <math>A_1, K, B_2</math> are collinear, so the three lines concur and we are done. | ||
| + | |||
| + | ~Leonard_my_dude | ||
Revision as of 14:00, 15 April 2021
Problem
Rectangles ![]()
![]() and
and ![]() are erected outside an acute triangle
are erected outside an acute triangle ![]() Suppose that
Suppose that![]() Prove that lines
Prove that lines ![]()
![]() and
and ![]() are concurrent.
are concurrent.
Solution
We first claim that the three circles ![]()
![]() and
and ![]() are share a common intersection.
are share a common intersection.
Let the second intersection of ![]() and
and ![]() be
be ![]() . Then
. Then
 which implies that
which implies that ![]() is cyclic as desired.
is cyclic as desired.
Now we show that ![]() is the intersection of
is the intersection of ![]()
![]() and
and ![]() Note that
Note that ![]() so
so ![]() are collinear. Similarly,
are collinear. Similarly, ![]() and
and ![]() are collinear, so the three lines concur and we are done.
are collinear, so the three lines concur and we are done.
~Leonard_my_dude