Difference between revisions of "2021 JMPSC Accuracy Problems/Problem 12"
(→Solution) |
(→Solution) |
||
| Line 6: | Line 6: | ||
==Solution== | ==Solution== | ||
| − | + | <center> | |
| − | [[File:Accuracy12sol.jpeg| | + | [[File:Accuracy12sol.jpeg|500px]] |
| − | + | </center> | |
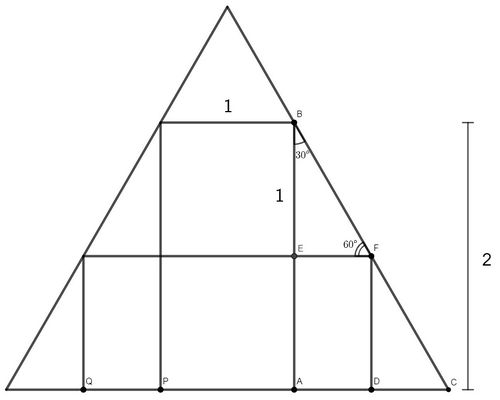
We are given <math>DF=1</math>, from which in rectangle <math>EFDA</math> we can conclude <math>AE=1</math>. Since <math>AB=2</math>, we have <cmath>AB-AE=2-1=1=BE.</cmath> | We are given <math>DF=1</math>, from which in rectangle <math>EFDA</math> we can conclude <math>AE=1</math>. Since <math>AB=2</math>, we have <cmath>AB-AE=2-1=1=BE.</cmath> | ||
Revision as of 22:17, 10 July 2021
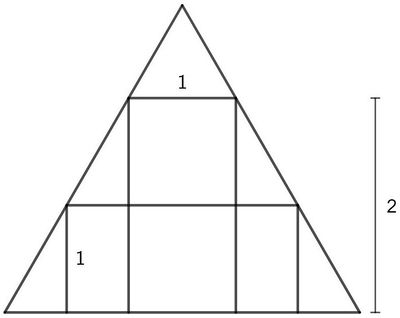
Problem
A rectangle with base ![]() and height
and height ![]() is inscribed in an equilateral triangle. Another rectangle with height
is inscribed in an equilateral triangle. Another rectangle with height ![]() is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction
is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction ![]() such that
such that ![]() Find
Find ![]() .
.
Solution
We are given ![]() , from which in rectangle
, from which in rectangle ![]() we can conclude
we can conclude ![]() . Since
. Since ![]() , we have
, we have ![]()
Since ![]() is parallel to
is parallel to ![]() and
and ![]() , we have that
, we have that ![]() by corresponding angles. Similarly,
by corresponding angles. Similarly, ![]() and it follows that
and it follows that ![]() is a
is a ![]() right triangle.
right triangle.
Since the side opposite the ![]() angle in
angle in ![]() is
is ![]() , we use our
, we use our ![]() ratios to find that
ratios to find that ![]() In rectangle
In rectangle ![]() , we also have
, we also have ![]() Analogously, we find that
Analogously, we find that ![]() Since we are looking for the base
Since we are looking for the base ![]() of the horizontal rectangle and we are given
of the horizontal rectangle and we are given ![]() we have
we have ![]() This gives us an answer of
This gives us an answer of ![]()