2021 JMPSC Accuracy Problems/Problem 12
Contents
[hide]Problem
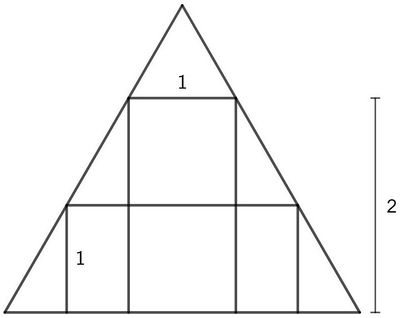
A rectangle with base ![]() and height
and height ![]() is inscribed in an equilateral triangle. Another rectangle with height
is inscribed in an equilateral triangle. Another rectangle with height ![]() is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction
is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction ![]() such that
such that ![]() Find
Find ![]() .
.
Solution
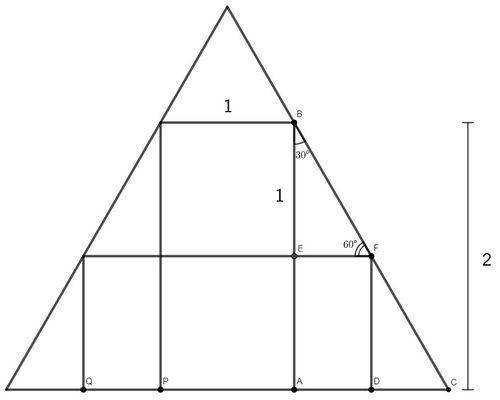
We are given ![]() , from which in rectangle
, from which in rectangle ![]() we can conclude
we can conclude ![]() . Since
. Since ![]() , we have
, we have ![]()
Since ![]() is parallel to
is parallel to ![]() and
and ![]() , we have that
, we have that ![]() by corresponding angles. Similarly,
by corresponding angles. Similarly, ![]() and it follows that
and it follows that ![]() is a
is a ![]() right triangle.
right triangle.
Since the side opposite the ![]() angle in
angle in ![]() is
is ![]() , we use our
, we use our ![]() ratios to find that
ratios to find that ![]() In rectangle
In rectangle ![]() , we also have
, we also have ![]() Analogously, we find that
Analogously, we find that ![]() Since we are looking for the base
Since we are looking for the base ![]() of the horizontal rectangle and we are given
of the horizontal rectangle and we are given ![]() we have
we have ![]() This gives us an answer of
This gives us an answer of ![]() ~ samrocksnature
~ samrocksnature
Solution 2
Since the angles of an equilateral triangle are ![]() , we have by similar triangles that the length of the segments of the "small" rectangles are
, we have by similar triangles that the length of the segments of the "small" rectangles are ![]() , meaning the answer is
, meaning the answer is ![]()
![]() ~Geometry285
~Geometry285
See also
The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition.