Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 JMPSC Accuracy Problems/Problem 12"

(→‎Solution)
(→‎Solution)
Line 13: Line 13:
 
Since <math>EF</math> is parallel to <math>AC</math> and <math>\angle C =60^\circ</math>, we have that <math>\angle BFE = 60^\circ</math> by corresponding angles. Similarly, <math>\angle BEF = 90^\circ</math> and it follows that <math>\triangle BFE</math> is a <math>30-60-90</math> right triangle.  
 
Since <math>EF</math> is parallel to <math>AC</math> and <math>\angle C =60^\circ</math>, we have that <math>\angle BFE = 60^\circ</math> by corresponding angles. Similarly, <math>\angle BEF = 90^\circ</math> and it follows that <math>\triangle BFE</math> is a <math>30-60-90</math> right triangle.  
  
−
Since the side opposite the <math>60^\circ</math> angle in <math>\triangle BFE</math> is <math>1</math>, we use our <math>30-60-90</math> ratios to find that <math>EF=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}.</math> In rectangle <math>EFDA</math>, we also have <cmath>AD=\frac{\sqrt{3}}{3}.</cmath> Analogously, we find that <cmath>QP=\frac{\sqrt{3}}{3}.</cmath> Since we are looking for the base <math>d</math> of the horizontal rectangle and we are given <cmath>PA=1,</cmath> we have <cmath>d=QP+PA+AD=\frac{\sqrt{3}}{3}+1+\frac{\sqrt{3}}{3}=\frac{3+2\sqrt{3}}{3}.</cmath> This gives us an answer of <math>2+3=\boxed{8}.</math> ~ samrocksnature
+
Since the side opposite the <math>60^\circ</math> angle in <math>\triangle BFE</math> is <math>1</math>, we use our <math>30-60-90</math> ratios to find that <math>EF=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}.</math> In rectangle <math>EFDA</math>, we also have <cmath>AD=\frac{\sqrt{3}}{3}.</cmath> Analogously, we find that <cmath>QP=\frac{\sqrt{3}}{3}.</cmath> Since we are looking for the base <math>d</math> of the horizontal rectangle and we are given <cmath>PA=1,</cmath> we have <cmath>d=QP+PA+AD=\frac{\sqrt{3}}{3}+1+\frac{\sqrt{3}}{3}=\frac{3+2\sqrt{3}}{3}.</cmath> This gives us an answer of <math>2+3+3=\boxed{8}.</math> ~ samrocksnature

Revision as of 10:47, 11 July 2021

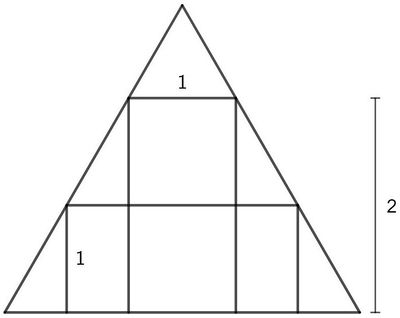
Problem

A rectangle with base $1$ and height $2$ is inscribed in an equilateral triangle. Another rectangle with height $1$ is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction $\frac{a+b\sqrt{3}}{c}$ such that $gcd(a,b,c)=1.$ Find $a+b+c$.

Sprint13.jpg

Solution

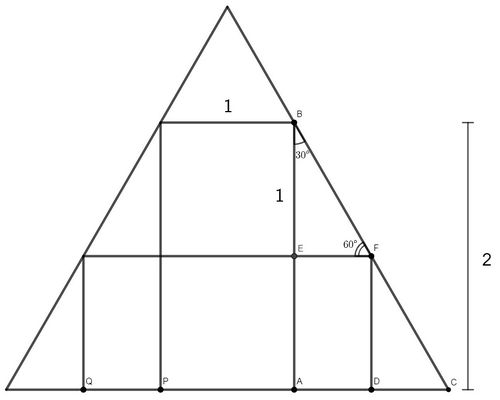
Accuracy12sol.jpeg

We are given $DF=1$, from which in rectangle $EFDA$ we can conclude $AE=1$. Since $AB=2$, we have \[AB-AE=2-1=1=BE.\]

Since $EF$ is parallel to $AC$ and $\angle C =60^\circ$, we have that $\angle BFE = 60^\circ$ by corresponding angles. Similarly, $\angle BEF = 90^\circ$ and it follows that $\triangle BFE$ is a $30-60-90$ right triangle.

Since the side opposite the $60^\circ$ angle in $\triangle BFE$ is $1$, we use our $30-60-90$ ratios to find that $EF=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}.$ In rectangle $EFDA$, we also have \[AD=\frac{\sqrt{3}}{3}.\] Analogously, we find that \[QP=\frac{\sqrt{3}}{3}.\] Since we are looking for the base $d$ of the horizontal rectangle and we are given \[PA=1,\] we have \[d=QP+PA+AD=\frac{\sqrt{3}}{3}+1+\frac{\sqrt{3}}{3}=\frac{3+2\sqrt{3}}{3}.\] This gives us an answer of $2+3+3=\boxed{8}.$ ~ samrocksnature

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_JMPSC_Accuracy_Problems/Problem_12&oldid=157847"