Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 JMPSC Accuracy Problems/Problem 12"

m
Line 19: Line 19:
 
<math>\linebreak</math>
 
<math>\linebreak</math>
 
~Geometry285
 
~Geometry285
 +
 +
==See also==
 +
#[[2021 JMPSC Sprint Problems|Other 2021 JMPSC Sprint Problems]]
 +
#[[2021 JMPSC Sprint Answer Key|2021 JMPSC Sprint Answer Key]]
 +
#[[JMPSC Problems and Solutions|All JMPSC Problems and Solutions]]
 +
{{JMPSC Notice}}

Revision as of 16:19, 11 July 2021

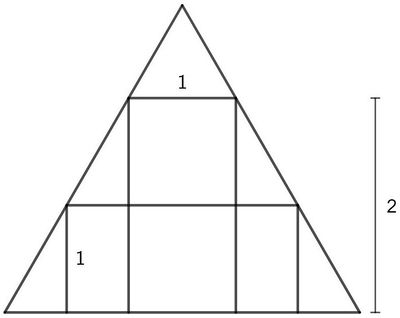
Problem

A rectangle with base $1$ and height $2$ is inscribed in an equilateral triangle. Another rectangle with height $1$ is also inscribed in the triangle. The base of the second rectangle can be written as a fully simplified fraction $\frac{a+b\sqrt{3}}{c}$ such that $gcd(a,b,c)=1.$ Find $a+b+c$.

Sprint13.jpg

Solution

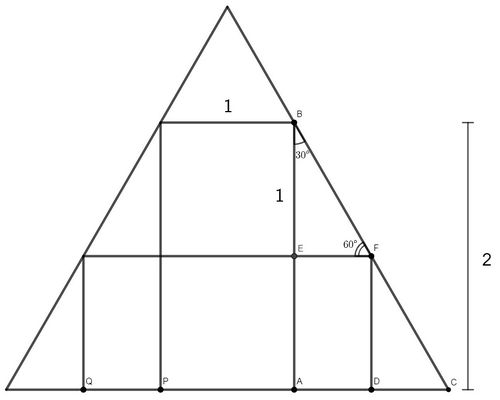
Accuracy12sol.jpeg

We are given $DF=1$, from which in rectangle $EFDA$ we can conclude $AE=1$. Since $AB=2$, we have \[AB-AE=2-1=1=BE.\]

Since $EF$ is parallel to $AC$ and $\angle C =60^\circ$, we have that $\angle BFE = 60^\circ$ by corresponding angles. Similarly, $\angle BEF = 90^\circ$ and it follows that $\triangle BFE$ is a $30-60-90$ right triangle.

Since the side opposite the $60^\circ$ angle in $\triangle BFE$ is $1$, we use our $30-60-90$ ratios to find that $EF=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}.$ In rectangle $EFDA$, we also have \[AD=\frac{\sqrt{3}}{3}.\] Analogously, we find that \[QP=\frac{\sqrt{3}}{3}.\] Since we are looking for the base $d$ of the horizontal rectangle and we are given \[PA=1,\] we have \[d=QP+PA+AD=\frac{\sqrt{3}}{3}+1+\frac{\sqrt{3}}{3}=\frac{3+2\sqrt{3}}{3}.\] This gives us an answer of $2+3+3=\boxed{8}.$ ~ samrocksnature

Solution 2

Since the angles of an equilateral triangle are $60^o$, we have by similar triangles that the length of the segments of the "small" rectangles are $\frac{\sqrt{3}}{3}$, meaning the answer is $\frac{3+2\sqrt{3}}{3} \implies 3+2+3=\boxed{8}$ $\linebreak$ ~Geometry285

See also

  1. Other 2021 JMPSC Sprint Problems
  2. 2021 JMPSC Sprint Answer Key
  3. All JMPSC Problems and Solutions

The problems on this page are copyrighted by the Junior Mathematicians' Problem Solving Competition. JMPSC.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_JMPSC_Accuracy_Problems/Problem_12&oldid=158047"