Difference between revisions of "1998 AIME Problems/Problem 9"
(problem/solution) |
(lines, wikify. Credit for 1st solution goes to joml88) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | Two mathematicians take a morning coffee break each day. They arrive at the cafeteria independently, at random times between 9 a.m. and 10 a.m., and stay for exactly <math>m</math> mintues. The probability that either one arrives while the other is in the cafeteria is <math>40 \%,</math> and <math>m = a - b\sqrt {c},</math> where <math>a, b,</math> and <math>c</math> are positive | + | Two mathematicians take a morning coffee break each day. They arrive at the cafeteria independently, at random times between 9 a.m. and 10 a.m., and stay for exactly <math>m</math> mintues. The [[probability]] that either one arrives while the other is in the cafeteria is <math>40 \%,</math> and <math>m = a - b\sqrt {c},</math> where <math>a, b,</math> and <math>c</math> are [[positive]] [[integer]]s, and <math>c</math> is not divisible by the square of any [[prime]]. Find <math>\displaystyle a + b + c.</math> |
__TOC__ | __TOC__ | ||
| Line 6: | Line 6: | ||
== Solution == | == Solution == | ||
=== Solution 1 === | === Solution 1 === | ||
| − | Let the two mathematicians be <math>M_1</math> and <math>M_2</math>. Consider plotting the times that they are on break on a coordinate plane and shading in the places where they would be there at the same time as such. | + | Let the two mathematicians be <math>M_1</math> and <math>M_2</math>. Consider plotting the times that they are on break on a [[coordinate plane]] and shading in the places where they would be there at the same time as such. |
We can count the area that we don't want in terms of <math>m</math> and solve: | We can count the area that we don't want in terms of <math>m</math> and solve: | ||
<div style="text-align:center;"> | <div style="text-align:center;"> | ||
| − | <math>\frac{(60-m)^2}{60^2} = .6</math> | + | <math>\frac{(60-m)^2}{60^2} = .6</math><br /> |
| − | <math>(60-m)^2 = 36\cdot 60</math> | + | <math>(60-m)^2 = 36\cdot 60</math><br /> |
| − | <math>60 - m = 12\sqrt{15}</math> | + | <math>60 - m = 12\sqrt{15}</math><br /> |
<math>\Rightarrow m = 60-12\sqrt{15}</math> | <math>\Rightarrow m = 60-12\sqrt{15}</math> | ||
</div> | </div> | ||
| Line 22: | Line 22: | ||
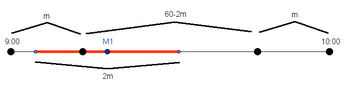
[[Image:AIME_1998-9b.png|350px]] | [[Image:AIME_1998-9b.png|350px]] | ||
| − | We draw a number line representing the time interval. If | + | We draw a [[number line]] representing the time interval. If mathematician <math>M_1</math> comes in at the center of the time period, then the two mathematicions will meet if <math>M_2</math> comes in somewhere between <math>m</math> minutes before and after <math>M_1</math> comes (a total range of <math>2m</math> minutes). However, if <math>M_1</math> comes into the cafeteria in the first or last <math>m</math> minutes, then the range in which <math>M_2</math> is reduced to somewhere in between <math>m</math> and <math>2m</math>. |
| − | We know try to find the weighted average of the chance that the two meet. In the central <math>\displaystyle 60-2m</math> minutes, <math>M_1</math> and <math>M_2</math> have to enter the cafeteria within <math>m</math> minutes of each other; so if we fix point <math>M_1</math> then <math>M_2</math> has a <math>\frac{2m}{60} = \frac{m}{30}</math> probability of meeting. | + | We know try to find the [[weighted average]] of the chance that the two meet. In the central <math>\displaystyle 60-2m</math> minutes, <math>M_1</math> and <math>M_2</math> have to enter the cafeteria within <math>m</math> minutes of each other; so if we fix point <math>M_1</math> then <math>M_2</math> has a <math>\frac{2m}{60} = \frac{m}{30}</math> probability of meeting. |
In the first and last <math>2m</math> minutes, the probability that the two meet ranges from <math>\frac{m}{60}</math> to <math>\frac{2m}{60}</math>, depending upon the location of <math>M_1</math> with respect to the endpoints. Intuitively, the average probability will occur at <math>\frac{\frac{3}{2}m}{60} = \frac{m}{40}</math>. | In the first and last <math>2m</math> minutes, the probability that the two meet ranges from <math>\frac{m}{60}</math> to <math>\frac{2m}{60}</math>, depending upon the location of <math>M_1</math> with respect to the endpoints. Intuitively, the average probability will occur at <math>\frac{\frac{3}{2}m}{60} = \frac{m}{40}</math>. | ||
Revision as of 10:08, 8 September 2007
Problem
Two mathematicians take a morning coffee break each day. They arrive at the cafeteria independently, at random times between 9 a.m. and 10 a.m., and stay for exactly ![]() mintues. The probability that either one arrives while the other is in the cafeteria is
mintues. The probability that either one arrives while the other is in the cafeteria is ![]() and
and ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
Contents
[hide]Solution
Solution 1
Let the two mathematicians be ![]() and
and ![]() . Consider plotting the times that they are on break on a coordinate plane and shading in the places where they would be there at the same time as such.
. Consider plotting the times that they are on break on a coordinate plane and shading in the places where they would be there at the same time as such.
We can count the area that we don't want in terms of ![]() and solve:
and solve:
![]()
![]()
![]()
![]()
So the answer is ![]() .
.
Solution 2
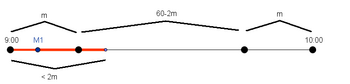
We draw a number line representing the time interval. If mathematician ![]() comes in at the center of the time period, then the two mathematicions will meet if
comes in at the center of the time period, then the two mathematicions will meet if ![]() comes in somewhere between
comes in somewhere between ![]() minutes before and after
minutes before and after ![]() comes (a total range of
comes (a total range of ![]() minutes). However, if
minutes). However, if ![]() comes into the cafeteria in the first or last
comes into the cafeteria in the first or last ![]() minutes, then the range in which
minutes, then the range in which ![]() is reduced to somewhere in between
is reduced to somewhere in between ![]() and
and ![]() .
.
We know try to find the weighted average of the chance that the two meet. In the central ![]() minutes,
minutes, ![]() and
and ![]() have to enter the cafeteria within
have to enter the cafeteria within ![]() minutes of each other; so if we fix point
minutes of each other; so if we fix point ![]() then
then ![]() has a
has a ![]() probability of meeting.
probability of meeting.
In the first and last ![]() minutes, the probability that the two meet ranges from
minutes, the probability that the two meet ranges from ![]() to
to ![]() , depending upon the location of
, depending upon the location of ![]() with respect to the endpoints. Intuitively, the average probability will occur at
with respect to the endpoints. Intuitively, the average probability will occur at ![]() .
.
So the weighted average is:
Solving this quadratic, we get two roots, ![]() . However,
. However, ![]() , so we discard the greater root; and thus our answer
, so we discard the greater root; and thus our answer ![]() .
.
See also
| 1998 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 8 |
Followed by Problem 10 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||