Difference between revisions of "2021 AMC 10A Problems/Problem 24"
Isabelchen (talk | contribs) |
Isabelchen (talk | contribs) m (→Solution 7 (Slope and Intercept)) |
||
| Line 135: | Line 135: | ||
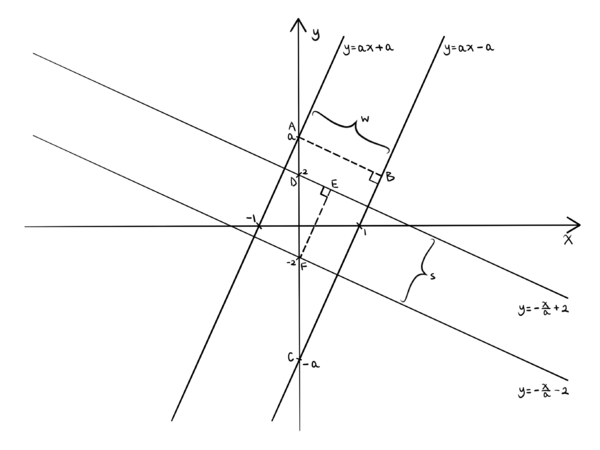
<math>DF = 4</math>, <math>DE = \sqrt{4^2 - s^2}</math> | <math>DF = 4</math>, <math>DE = \sqrt{4^2 - s^2}</math> | ||
| − | Because the slope of line <math>y = ax - a</math> is <math>a</math>, <math>\frac{s}{\sqrt{16-s^2}} | + | Because the slope of line <math>y = ax - a</math> is <math>a</math>, <math>a = \frac{EF}{DE} = \frac{s}{\sqrt{16-s^2}}</math>, <math>s^2(a^2+1) = 16a^2</math>, <math>s = \frac{4a}{\sqrt{a^2+1}}</math> |
<math>AC = 2a</math>, <math>BC = \sqrt{(2a)^2 - w^2}</math> | <math>AC = 2a</math>, <math>BC = \sqrt{(2a)^2 - w^2}</math> | ||
| − | Because the slope of line <math>y = ax - a</math> is <math>a</math>, <math>\frac{\sqrt{4a^2-w^2}}{w} | + | Because the slope of line <math>y = ax - a</math> is <math>a</math>, <math>a = \frac{BC}{AB} = \frac{\sqrt{4a^2-w^2}}{w}</math>, <math>w^2(a^2+1)=4a^2</math>, <math>w=\frac{2a}{\sqrt{a^2+1}}</math> |
| − | <math> | + | <math>\text{Area} = s \cdot w=\frac{4a}{\sqrt{a^2+1}} \cdot \frac{2a}{\sqrt{a^2+1}} = \boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}</math> |
~isabelchen | ~isabelchen | ||
Revision as of 07:11, 26 December 2021
Contents
[hide]- 1 Problem
- 2 Diagram
- 3 Solution 1 (Generalized Value of a)
- 4 Solution 2 (Specified Value of a)
- 5 Solution 3 (Trigonometry)
- 6 Solution 4 (Observations)
- 7 Solution 5 (Observations)
- 8 Solution 6 (Observations: Cheap)
- 9 Solution 7 (Slope and Intercept)
- 10 Video Solution by OmegaLearn (System of Equations and Shoelace Formula)
- 11 Video Solution by MRENTHUSIASM (English & Chinese)
- 12 See also
Problem
The interior of a quadrilateral is bounded by the graphs of ![]() and
and ![]() , where
, where ![]() is a positive real number. What is the area of this region in terms of
is a positive real number. What is the area of this region in terms of ![]() , valid for all
, valid for all ![]() ?
?
![]()
Diagram
Graph in Desmos: https://www.desmos.com/calculator/satawguqsc
~MRENTHUSIASM
Solution 1 (Generalized Value of a)
The cases for ![]() are
are ![]() or two parallel lines. We rearrange each case and construct the table below:
or two parallel lines. We rearrange each case and construct the table below:
![\[\begin{array}{c||c|c|c|c} & & & & \\ [-2.5ex] \textbf{Case} & \textbf{Line's Equation} & \boldsymbol{x}\textbf{-intercept} & \boldsymbol{y}\textbf{-intercept} & \textbf{Slope} \\ [0.5ex] \hline & & & & \\ [-1.5ex] 1 & x+ay-2a=0 & 2a & 2 & -\frac1a \\ [2ex] 2 & x+ay+2a=0 & -2a & -2 & -\frac1a \\ [0.75ex] \end{array}\]](http://latex.artofproblemsolving.com/d/3/1/d310eb29709b064a232dcde1051f451297bcc5c7.png) The cases for
The cases for ![]() are
are ![]() or two parallel lines. We rearrange each case and construct the table below:
or two parallel lines. We rearrange each case and construct the table below:
![\[\begin{array}{c||c|c|c|c} & & & & \\ [-2.5ex] \textbf{Case} & \textbf{Line's Equation} & \boldsymbol{x}\textbf{-intercept} & \boldsymbol{y}\textbf{-intercept} & \textbf{Slope} \\ [0.5ex] \hline & & & & \\ [-1.5ex] 1* & ax-y-a=0 & 1 & -a & a \\ [2ex] 2* & ax-y+a=0 & -1 & a & a \\ [0.75ex] \end{array}\]](http://latex.artofproblemsolving.com/d/6/2/d621933287f3026fd25738ef5776799dc4f8923f.png) Since the slopes of intersecting lines
Since the slopes of intersecting lines ![]() and
and ![]() are negative reciprocals, we get four right angles, from which the quadrilateral is a rectangle.
are negative reciprocals, we get four right angles, from which the quadrilateral is a rectangle.
Two solutions follow from here:
Solution 1.1 (Distance Between Parallel Lines)
Recall that for constants ![]() and
and ![]() the distance
the distance ![]() between parallel lines
between parallel lines
 is
is ![]() From this formula:
From this formula:
- The distance between lines
 and
and  is
is  the length of this rectangle.
the length of this rectangle.
- The distance between lines
 and
and  is
is  the width of this rectangle.
the width of this rectangle.
The area we seek is ![\[\frac{4a}{\sqrt{1+a^2}}\cdot\frac{2a}{\sqrt{a^2+1}}=\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.\]](http://latex.artofproblemsolving.com/5/0/e/50e435068cd851070a2d7aff8a2ed8dd670e5c6b.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1.2 (Distance Between Points)
The solutions to systems of equations ![]() are
are ![]() respectively, which are the consecutive vertices of this rectangle.
respectively, which are the consecutive vertices of this rectangle.
By the Distance Formula, the length and width of this rectangle are ![]() and
and ![]() respectively.
respectively.
The area we seek is ![\[\frac{4a\sqrt{a^2+1}}{a^2+1}\cdot\frac{2a\sqrt{a^2+1}}{a^2+1}=\boxed{\textbf{(D)} ~\frac{8a^2}{a^2+1}}.\]](http://latex.artofproblemsolving.com/b/5/5/b55864fdf698bbccc132eff11aea2d658eeb171d.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 2 (Specified Value of a)
In this solution, we will refer to equations ![]() and
and ![]() from Solution 1.
from Solution 1.
Substituting ![]() into the answer choices gives
into the answer choices gives
![]()
At ![]() the solutions to systems of equations
the solutions to systems of equations ![]() are
are ![]() respectively, which are the consecutive vertices of the quadrilateral.
respectively, which are the consecutive vertices of the quadrilateral.
Two solutions follow from here:
Solution 2.1 (Area of a Rectangle)
From the tables in Solution 1, we conclude that the quadrilateral is a rectangle.
By the Distance Formula, the length and width of this rectangle are ![]() and
and ![]() respectively.
respectively.
The area we seek is ![]() from which the answer is
from which the answer is 
~MRENTHUSIASM
Solution 2.2 (Area of a General Quadrilateral)
Even if we do not recognize that the quadrilateral is a rectangle, we can apply the Shoelace Theorem to its consecutive vertices
 The area we seek is
The area we seek is ![]() from which the answer is
from which the answer is 
~MRENTHUSIASM
Solution 3 (Trigonometry)
Similar to Solution 1, we will use the equations from the four cases:
 This is a line with
This is a line with  -intercept
-intercept 
 -intercept
-intercept  and slope
and slope 
 This is a line with
This is a line with  -intercept
-intercept 
 -intercept
-intercept  and slope
and slope 
 This is a line with
This is a line with  -intercept
-intercept 
 -intercept
-intercept  and slope
and slope 
 This is a line with
This is a line with  -intercept
-intercept 
 -intercept
-intercept  and slope
and slope 
Let ![]() The area of the rectangle created by the four equations can be written as
The area of the rectangle created by the four equations can be written as
 ~fnothing4994 (Solution)
~fnothing4994 (Solution)
~MRENTHUSIASM (Code Adjustments)
Solution 4 (Observations)
The conditions ![]() and
and ![]() give
give ![]() and
and ![]() or
or ![]() and
and ![]() . The slopes here are perpendicular, so the quadrilateral is a rectangle.
Plug in
. The slopes here are perpendicular, so the quadrilateral is a rectangle.
Plug in ![]() and graph it. We quickly see that the area is
and graph it. We quickly see that the area is ![]() , so the answer can't be
, so the answer can't be ![]() or
or ![]() by testing the values they give (test it!). Now plug in
by testing the values they give (test it!). Now plug in ![]() . We see using a ruler that the sides of the rectangle are about
. We see using a ruler that the sides of the rectangle are about ![]() and
and ![]() . So the area is about
. So the area is about ![]() . Testing
. Testing ![]() , we get
, we get ![]() which is clearly less than
which is clearly less than ![]() , so it is out. Testing
, so it is out. Testing ![]() , we get
, we get ![]() which is near our answer, so we leave it. Testing
which is near our answer, so we leave it. Testing ![]() , we get
, we get ![]() , way less than
, way less than ![]() , so it is out. So, the only plausible answer is
, so it is out. So, the only plausible answer is  .
.
~firebolt360
Solution 5 (Observations)
Trying ![]() narrows down the choices to options
narrows down the choices to options ![]() ,
, ![]() and
and ![]() . Trying
. Trying ![]() and
and ![]() eliminates
eliminates ![]() and
and ![]() , to obtain
, to obtain  as our answer. Refer to Solution 2 for a detailed explanation.
as our answer. Refer to Solution 2 for a detailed explanation.
~¢
Solution 6 (Observations: Cheap)
Note that ![]() yields different values for all answer choices. If we put in
yields different values for all answer choices. If we put in ![]() we find that the area of the quadrilateral is
we find that the area of the quadrilateral is ![]() This means that the answer must be
This means that the answer must be  Refer to Solution 2 for a detailed explanation.
Refer to Solution 2 for a detailed explanation.
Solution 7 (Slope and Intercept)
The quadrilateral is enclosed by ![]() lines:
lines:
![]()
![]()
![]() ,
, ![]() intercept:
intercept: ![]() ,
, ![]() intercept:
intercept: ![]() , slope:
, slope:![]()
![]()
![]()
![]() ,
, ![]() intercept:
intercept: ![]() ,
, ![]() intercept:
intercept: ![]() , slope:
, slope:![]()
![]()
![]()
![]() ,
, ![]() intercept:
intercept: ![]() ,
, ![]() intercept:
intercept: ![]() , slope:
, slope:![]()
![]()
![]()
![]() ,
, ![]() intercept:
intercept: ![]() ,
, ![]() intercept:
intercept: ![]() , slope:
, slope:![]()
![]() ,
, ![]()
Because the slope of line ![]() is
is ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]()
Because the slope of line ![]() is
is ![]() ,
, ![]() ,
, ![]() ,
, ![]()

~isabelchen
Video Solution by OmegaLearn (System of Equations and Shoelace Formula)
~ pi_is_3.14
Video Solution by MRENTHUSIASM (English & Chinese)
https://www.youtube.com/watch?v=oEY-kX4d87M
~MRENTHUSIASM
See also
| 2021 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 23 |
Followed by Problem 25 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()