Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 IMO Problems/Problem 3"

(→‎Problem)
(→‎Solution)
Line 3: Line 3:
  
 
==Solution==
 
==Solution==
 +
[[File:2021 IMO 3.png|450px|right]]
 
<i><b>Lemma</b></i>
 
<i><b>Lemma</b></i>
  
 
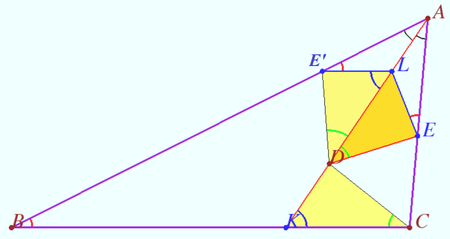
Let <math>AK</math> be bisector of the triangle <math>ABC</math>, point <math>D</math> lies on <math>AK.</math> The point <math>E</math> on the segment <math>AC</math> satisfies <math>\angle ADE= \angle BCD</math>. The point <math>E'</math> is symmetric to <math>E</math> with respect to <math>AK.</math> The point <math>L</math> on the segment <math>AK</math>  satisfies <math>E'L||BC.</math>
 
Let <math>AK</math> be bisector of the triangle <math>ABC</math>, point <math>D</math> lies on <math>AK.</math> The point <math>E</math> on the segment <math>AC</math> satisfies <math>\angle ADE= \angle BCD</math>. The point <math>E'</math> is symmetric to <math>E</math> with respect to <math>AK.</math> The point <math>L</math> on the segment <math>AK</math>  satisfies <math>E'L||BC.</math>
 
Then <math>EL</math> and <math>BC</math> are antiparallel with respect to the sides of an angle <math>A</math> and <cmath>\frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.</cmath>
 
Then <math>EL</math> and <math>BC</math> are antiparallel with respect to the sides of an angle <math>A</math> and <cmath>\frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.</cmath>
 +
<i><b>Proof</b></i>
 +
 +
Symmetry of points <math>E</math> and <math>E'</math> with respect bisector <math>AK</math> implies <math>\angle AEL = \angle AE'L.</math>
 +
<cmath>\angle DCK = \angle E'DL,  \angle DKC = \angle E'LD \implies \triangle DCK \sim \triangle E'DL \implies \frac {E'L}{KD}=  \frac {DL}{KC}.</cmath>
 +
<cmath>\triangle ALE' \sim \triangle AKB \implies \frac {E'L}{BK}=  \frac {AL}{AK}\implies \frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.</cmath>
  
 
==Video solution==
 
==Video solution==
 
https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems]
 
https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems]

Revision as of 19:43, 9 July 2022

Problem

Let $D$ be an interior point of the acute triangle $ABC$ with $AB > AC$ so that $\angle DAB= \angle CAD$. The point $E$ on the segment $AC$ satisfies $\angle ADE= \angle BCD$, the point $F$ on the segment $AB$ satisfies $\angle FDA= \angle DBC$, and the point $X$ on the line $AC$ satisfies $CX=BX$. Let $O_1$ and $O_2$ be the circumcentres of the triangles $ADC$ and $EXD$ respectively. Prove that the lines $BC$, $EF$, and $O_1 O_2$ are concurrent.

Solution

2021 IMO 3.png

Lemma

Let $AK$ be bisector of the triangle $ABC$, point $D$ lies on $AK.$ The point $E$ on the segment $AC$ satisfies $\angle ADE= \angle BCD$. The point $E'$ is symmetric to $E$ with respect to $AK.$ The point $L$ on the segment $AK$ satisfies $E'L||BC.$ Then $EL$ and $BC$ are antiparallel with respect to the sides of an angle $A$ and \[\frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.\] Proof

Symmetry of points $E$ and $E'$ with respect bisector $AK$ implies $\angle AEL = \angle AE'L.$ \[\angle DCK = \angle E'DL, \angle DKC = \angle E'LD \implies \triangle DCK \sim \triangle E'DL \implies \frac {E'L}{KD}= \frac {DL}{KC}.\] \[\triangle ALE' \sim \triangle AKB \implies \frac {E'L}{BK}= \frac {AL}{AK}\implies \frac {AL}{DL} = \frac {AK \cdot DK}{BK \cdot KC}.\]

Video solution

https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems]

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_IMO_Problems/Problem_3&oldid=175765"