2021 IMO Problems/Problem 3
Contents
[hide]Problem
Let ![]() be an interior point of the acute triangle
be an interior point of the acute triangle ![]() with
with ![]() so that
so that ![]() . The point
. The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() , the point
, the point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() , and the point
, and the point ![]() on the line
on the line ![]() satisfies
satisfies ![]() . Let
. Let ![]() and
and ![]() be the circumcentres of the triangles
be the circumcentres of the triangles ![]() and
and ![]() respectively. Prove that the lines
respectively. Prove that the lines ![]() ,
, ![]() , and
, and ![]() are concurrent.
are concurrent.
Solution
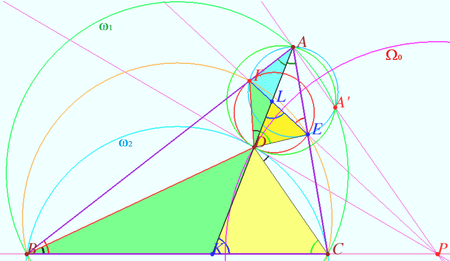
We prove that circles ![]() and
and ![]() centered at
centered at ![]() (the intersection point
(the intersection point ![]() and
and ![]() have a common chord.
have a common chord.
Let ![]() be the intersection point of the tangent to the circle
be the intersection point of the tangent to the circle ![]() at the point
at the point ![]() and the line
and the line ![]() is inverse to
is inverse to ![]() with respect to the circle
with respect to the circle ![]() centered at
centered at ![]() with radius
with radius ![]() Then the pairs of points
Then the pairs of points ![]() and
and ![]() and
and ![]() are inverse with respect to
are inverse with respect to ![]() , so the points
, so the points ![]() and
and ![]() are collinear. Quadrilaterals containing the pairs of inverse points
are collinear. Quadrilaterals containing the pairs of inverse points ![]() and
and ![]() and
and ![]() and
and ![]() are inscribed,
are inscribed, ![]() is antiparallel to
is antiparallel to ![]() with respect to angle
with respect to angle ![]() (see
(see ![]() ).
).
Consider the circles ![]() centered at
centered at ![]()
![]() centered at
centered at ![]() and
and ![]()
Denote ![]() . Then
. Then ![]()
![]() is cyclic),
is cyclic),
![]() is cyclic,
is cyclic, ![]() is antiparallel),
is antiparallel),
![]()
![]() is the point of the circle
is the point of the circle ![]()
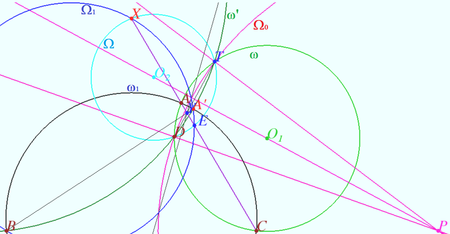
Let the point ![]() be the radical center of the circles
be the radical center of the circles ![]() It has the same power
It has the same power ![]() with respect to these circles. The common chords of the pairs of circles
with respect to these circles. The common chords of the pairs of circles ![]() where
where ![]() intersect at this point.
intersect at this point.
![]() has power
has power ![]() with respect to
with respect to ![]() since
since ![]() is the radical axis of
is the radical axis of ![]()
![]() has power
has power ![]() with respect to
with respect to ![]() since
since ![]() containing
containing ![]() is the radical axis of
is the radical axis of ![]() and
and ![]() Hence
Hence ![]() has power
has power ![]() with respect to
with respect to ![]()
Let ![]() be the point of intersection
be the point of intersection ![]() Since the circles
Since the circles ![]() and
and ![]() are inverse with respect to
are inverse with respect to ![]() then
then ![]() lies on
lies on ![]() and
and ![]() lies on the perpendicular bisector of
lies on the perpendicular bisector of ![]() The power of a point
The power of a point ![]() with respect to the circles
with respect to the circles ![]() and
and ![]() are the same,
are the same, ![]() the points
the points ![]() and
and ![]() coincide.
coincide.
The centers of the circles ![]() and
and ![]() (
(![]() and
and ![]() ) are located on the perpendicular bisector
) are located on the perpendicular bisector ![]() , the point
, the point ![]() is located on the perpendicular bisector
is located on the perpendicular bisector ![]() and, therefore, the points
and, therefore, the points ![]() and
and ![]() lie on a line, that is, the lines
lie on a line, that is, the lines ![]() and
and ![]() are concurrent.
are concurrent.
![]()
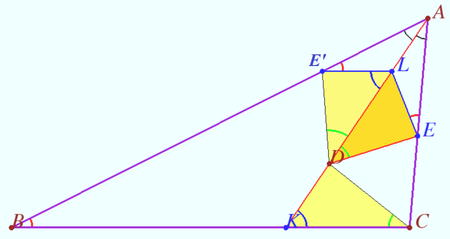
Let ![]() be bisector of the triangle
be bisector of the triangle ![]() , point
, point ![]() lies on
lies on ![]() The point
The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() . The point
. The point ![]() on the segment
on the segment ![]() satisfies
satisfies ![]() Let
Let ![]() be the intersection point of the tangent to the circle
be the intersection point of the tangent to the circle ![]() at the point
at the point ![]() and the line
and the line ![]() Let the circle
Let the circle ![]() be centered at
be centered at ![]() and has the radius
and has the radius ![]()
Then the pairs of points ![]() and
and ![]() and
and ![]() are inverse with respect to
are inverse with respect to ![]() and
and ![]() and
and ![]() are antiparallel with respect to the sides of an angle
are antiparallel with respect to the sides of an angle ![]()
![]()
Let the point ![]() is symmetric to
is symmetric to ![]() with respect to bisector
with respect to bisector ![]() Symmetry of points
Symmetry of points ![]() and
and ![]() implies
implies ![]()
![]()
![]()
![]()
![]() Similarly, we prove that
Similarly, we prove that ![]() and
and ![]() are antiparallel with respect to angle
are antiparallel with respect to angle ![]() and the points
and the points ![]() in triangles
in triangles ![]() and
and ![]() coincide. Hence,
coincide. Hence, ![]() and
and ![]() are antiparallel and
are antiparallel and ![]() is cyclic.
Note that
is cyclic.
Note that ![]() and
and
![]()
![]() so
so ![]() is tangent to the circle
is tangent to the circle ![]()
![]() that is, the points
that is, the points ![]() and
and ![]() and
and ![]() are inverse with respect to the circle
are inverse with respect to the circle ![]()
vladimir.shelomovskii@gmail.com, vvsss
Video solution
https://youtu.be/cI9p-Z4-Sc8 [Video contains solutions to all day 1 problems]
See also
| 2021 IMO (Problems) • Resources | ||
| Preceded by Problem 2 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Problem 4 |
| All IMO Problems and Solutions | ||