Difference between revisions of "2018 IMO Problems/Problem 6"
(→Solution) |
(→Solution) |
||
| Line 47: | Line 47: | ||
[[File:2018 IMO 6bb.png|430px|right]] | [[File:2018 IMO 6bb.png|430px|right]] | ||
[[File:2018 IMO 6c.png|430px|right]] | [[File:2018 IMO 6c.png|430px|right]] | ||
| + | [[File:2018 IMO 6d.png|430px|right]] | ||
<i><b>Common case </b></i> | <i><b>Common case </b></i> | ||
| Line 69: | Line 70: | ||
Quadrangle <math>AYCD</math> is cyclic <math>\implies \angle YAD = \angle BCY.</math> | Quadrangle <math>AYCD</math> is cyclic <math>\implies \angle YAD = \angle BCY.</math> | ||
| − | The triangles <math>\triangle YAD \sim \triangle YCD</math> by two angles, so <cmath>\frac {BC}{AD} = \frac {CY}{AY} = \frac {BY} {DY}.</cmath> | + | The triangles <math>\triangle YAD \sim \triangle YCD</math> by two angles, so <cmath>\frac {BC}{AD} = \frac {CY}{AY} = \frac {BY} {DY} \hspace{10mm} (1).</cmath> |
The points <math>X</math> and <math>Y</math> are symmetric with respect to the circle <math>\omega</math>, since they lie on the intersection of the circles <math>ACF</math> and <math>ACE</math> symmetric with respect to <math>\omega</math> and the orthogonal <math>\omega</math> circle <math>BDE.</math> | The points <math>X</math> and <math>Y</math> are symmetric with respect to the circle <math>\omega</math>, since they lie on the intersection of the circles <math>ACF</math> and <math>ACE</math> symmetric with respect to <math>\omega</math> and the orthogonal <math>\omega</math> circle <math>BDE.</math> | ||
The point <math>C</math> is symmetric to itself, the point <math>X</math> is symmetric to <math>Y</math> with respect to <math>\omega \implies \frac{CX}{CY} = \frac {R^2}{OC \cdot OY} , \frac {AX}{AY} = \frac {R^2}{OA \cdot OY}.</math> | The point <math>C</math> is symmetric to itself, the point <math>X</math> is symmetric to <math>Y</math> with respect to <math>\omega \implies \frac{CX}{CY} = \frac {R^2}{OC \cdot OY} , \frac {AX}{AY} = \frac {R^2}{OA \cdot OY}.</math> | ||
| + | Usung <math>(1)</math> and the equality <math>OA = OC,</math> we get <cmath>\frac{CY}{AY} = \frac {CX}{AX} = \frac{BC}{AD}.</cmath> | ||
| + | The point <math>C</math> is symmetric to itself, the point <math>B</math> is symmetric to <math>D</math> with respect to <math>\omega \implies</math> | ||
| + | <cmath>\triangle OBC \sim \triangle OCD \implies \frac {OB}{OC} = \frac {BC}{CD} = \frac {OC}{OD},</cmath> | ||
| + | <cmath>\frac {OB}{OD} = \frac {OB}{OC} \cdot \frac {OC}{OD} = \frac{BC^2}{CD^2} = \frac{BC}{CD} \cdot \frac {AB}{AD}.</cmath> | ||
| + | The point <math>B</math> is symmetric to <math>D</math> and the point <math>X</math> is symmetric to <math>Y</math> with respect to <math>\omega,</math> hence | ||
| + | <cmath>\frac {BX}{DY} = \frac {R^2}{OD \cdot OY} ,\frac {DX}{BY} = \frac{R^2}{OB \cdot OY}.</cmath> | ||
| + | <cmath>\frac{BX}{DX} =\frac{DY}{BY} \cdot \frac {OB}{OD} = \frac{AD}{BC} \cdot \frac{BC}{CD} \cdot \frac{AB}{AD} = \frac{AB}{CD}.</cmath> | ||
| + | Denote <math>\angle XAB = \angle XCD = \alpha, \angle BXA = \varphi, \angle DXC = \psi.</math> | ||
| + | |||
| + | By the law of sines for the <math>\triangle ABX,</math> we obtain <math>\frac {AB}{\sin \varphi} = \frac{BX}{\sin \alpha}.</math> | ||
Revision as of 07:56, 19 August 2022
A convex quadrilateral ![]() satisfies
satisfies ![]() Point
Point ![]() lies inside
lies inside
![]() so that
so that
![]() and
and ![]() Prove that
Prove that ![]()
Solution
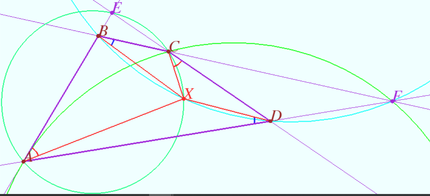
Special case
We construct point ![]() and prove that
and prove that ![]() coincides with the point
coincides with the point ![]()
Let ![]() and
and ![]()
Let ![]() and
and ![]() be the intersection points of
be the intersection points of ![]() and
and ![]() and
and ![]() and
and ![]() respectively.
respectively.
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circle ![]() is orthogonal to the circle
is orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Let ![]() be the point of intersection of the circles
be the point of intersection of the circles ![]() and
and ![]() Quadrilateral
Quadrilateral ![]() is cyclic
is cyclic ![]()
![]()
Similarly, quadrangle ![]() is cyclic
is cyclic ![]() .
.
This means that point ![]() coincides with the point
coincides with the point ![]() .
.
![]() of
of ![]()
![]() of
of ![]()
The sum ![]() (Claim 3)
(Claim 3) ![]()
![]()
Similarly, ![]()
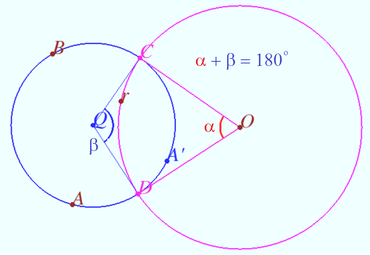
Claim 1 Let ![]() and
and ![]() be arbitrary points on a circle
be arbitrary points on a circle ![]() be the middle perpendicular to the segment
be the middle perpendicular to the segment ![]() Then the straight lines
Then the straight lines ![]() and
and ![]() intersect
intersect ![]() at the points
at the points ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]()
Claim 2 Let points ![]() and
and ![]() be symmetric with respect to the circle
be symmetric with respect to the circle ![]() Then any circle
Then any circle ![]() passing through these points is orthogonal to
passing through these points is orthogonal to ![]()
Claim 3 The sum of the arcs between the points of intersection of two perpendicular circles is ![]() In the figure they are a blue and red arcs
In the figure they are a blue and red arcs ![]()
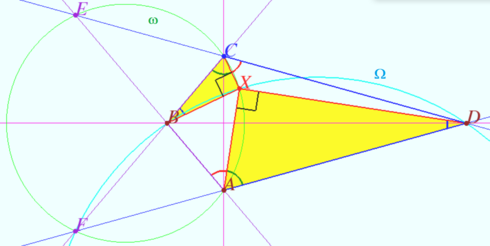
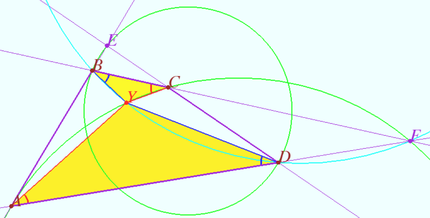
Common case
Denote by ![]() the intersection point of the perpendicular bisector of
the intersection point of the perpendicular bisector of ![]() and
and ![]() Let
Let ![]() be a circle (red) with center
be a circle (red) with center ![]() and radius
and radius ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circles ![]() and
and ![]() are orthogonal to the circle
are orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Circles ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Lemma).
(Lemma).
Denote by ![]() the point of intersection of the circles
the point of intersection of the circles ![]() and
and ![]() Quadrangle
Quadrangle ![]() is cyclic
is cyclic ![]() (see Special case).
Similarly, quadrangle
(see Special case).
Similarly, quadrangle ![]() is cyclic
is cyclic ![]()
The required point ![]() is constructed.
is constructed.
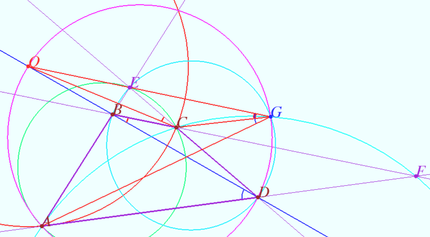
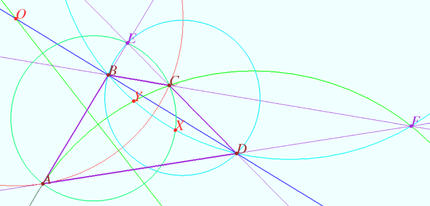
Denote by ![]() the point of intersection of circles
the point of intersection of circles ![]() and
and ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
The triangles ![]() by two angles, so
by two angles, so ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() , since they lie on the intersection of the circles
, since they lie on the intersection of the circles ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]() and the orthogonal
and the orthogonal ![]() circle
circle ![]()
The point ![]() is symmetric to itself, the point
is symmetric to itself, the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() Usung
Usung ![]() and the equality
and the equality ![]() we get
we get ![]() The point
The point ![]() is symmetric to itself, the point
is symmetric to itself, the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
![]()
![]() The point
The point ![]() is symmetric to
is symmetric to ![]() and the point
and the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() hence
hence
![]()
![]() Denote
Denote ![]()
By the law of sines for the ![]() we obtain
we obtain ![]()