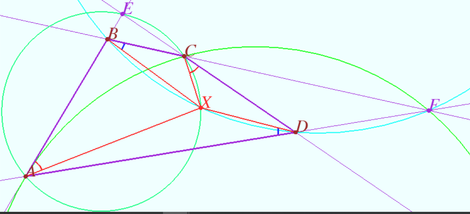
2018 IMO Problems/Problem 6
Problem
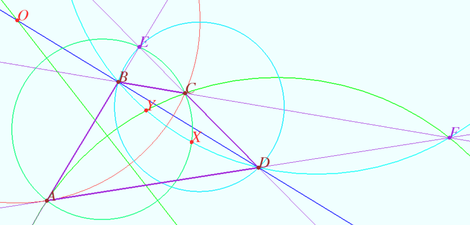
A convex quadrilateral ![]() satisfies
satisfies ![]() Point
Point ![]() lies inside
lies inside
![]() so that
so that
![]() and
and ![]() Prove that
Prove that ![]()
Solution
We want to find the point ![]() Let
Let ![]() and
and ![]() be the intersection points of
be the intersection points of ![]() and
and ![]() and
and ![]() and
and ![]() respectively.
The poinx
respectively.
The poinx ![]() is inside
is inside ![]() so points
so points ![]() follow in this order.
follow in this order.
![]()
![]() is cyclic
is cyclic ![]() lie on circle
lie on circle ![]()
Similarly, ![]() lie on circle
lie on circle ![]()
Point ![]() is the point of intersection of circles
is the point of intersection of circles ![]() and
and ![]()
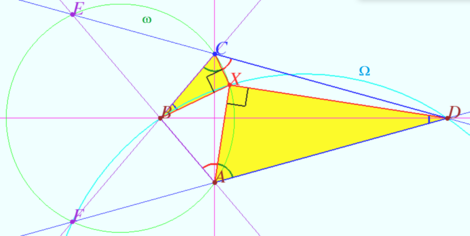
Special case
Let ![]() and
and ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Claim 1).
(Claim 1).
The circle ![]() is orthogonal to the circle
is orthogonal to the circle ![]() (Claim 2).
(Claim 2).
![]() of
of ![]()
![]() of
of ![]()
![]() (Claim 3)
(Claim 3) ![]()
![]()
Similarly, ![]()
![]()
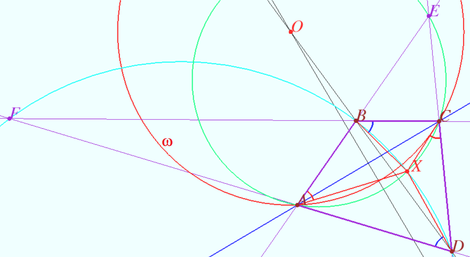
Common case
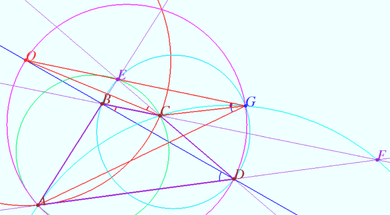
Denote by ![]() the intersection point of
the intersection point of ![]() and the perpendicular bisector of
and the perpendicular bisector of ![]() Let
Let ![]() be a circle (red) with center
be a circle (red) with center ![]() and radius
and radius ![]()
We will prove ![]() using point
using point ![]() symmetric to
symmetric to ![]() with respect to
with respect to ![]()
The points ![]() and
and ![]() are symmetric with respect to
are symmetric with respect to ![]() (Claim 1).
(Claim 1).
The circles ![]() and
and ![]() are orthogonal to the circle
are orthogonal to the circle ![]() (Claim 2).
(Claim 2).
Circles ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (Lemma).
(Lemma).
Denote by ![]() the point of intersection of circles
the point of intersection of circles ![]() and
and ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
Quadrangle ![]() is cyclic
is cyclic ![]()
The triangles ![]() by two angles, so
by two angles, so ![]()
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() , since they lie on the intersection of the circles
, since they lie on the intersection of the circles ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]() and the circle
and the circle ![]() orthogonal to
orthogonal to ![]()
The point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]()
![]()
![]() The point
The point ![]() is symmetric to
is symmetric to ![]() and the point
and the point ![]() is symmetric to
is symmetric to ![]() with respect to
with respect to ![]() hence
hence
![]()
![]()
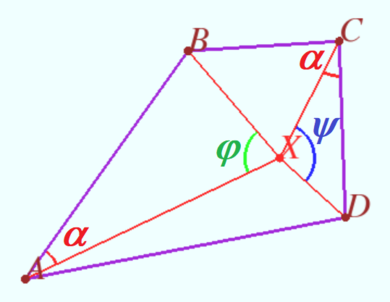
Denote ![]()
By the law of sines for ![]() we obtain
we obtain ![]()
By the law of sines for ![]() we obtain
we obtain ![]()
Hence we get ![]()
If ![]() then
then ![]()
![]() This is a special case.
This is a special case.
In all other cases, the equality of the sines follows ![]()
Claim 1 Let ![]() and
and ![]() be arbitrary points on a circle
be arbitrary points on a circle ![]() be the perpendicular bisector to the segment
be the perpendicular bisector to the segment ![]() Then the straight lines
Then the straight lines ![]() and
and ![]() intersect
intersect ![]() at the points
at the points ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]()
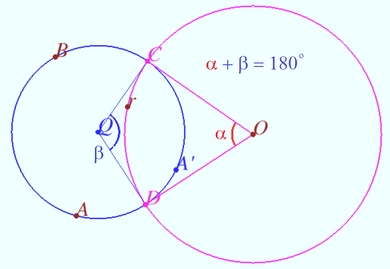
Claim 2 Let points ![]() and
and ![]() be symmetric with respect to the circle
be symmetric with respect to the circle ![]() Then any circle
Then any circle ![]() passing through these points is orthogonal to
passing through these points is orthogonal to ![]()
Claim 3 The sum of the arcs between the points of intersection of two perpendicular circles is ![]() In the figure they are a blue and red arcs
In the figure they are a blue and red arcs ![]()
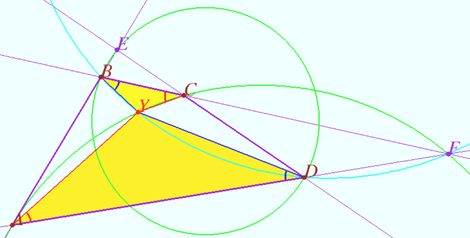
Lemma The opposite sides of the quadrilateral ![]() intersect at points
intersect at points ![]() and
and ![]() (
(![]() lies on
lies on ![]() ). The circle
). The circle ![]() centered at the point
centered at the point ![]() contains the ends of the diagonal
contains the ends of the diagonal ![]() The points
The points ![]() and
and ![]() are symmetric with respect to the circle
are symmetric with respect to the circle ![]() (in other words, the inversion with respect to
(in other words, the inversion with respect to ![]() maps
maps ![]() into
into ![]() Then the circles
Then the circles ![]() and
and ![]() are symmetric with respect to
are symmetric with respect to ![]()
Proof We will prove that the point ![]() symmetric to the point
symmetric to the point ![]() with respect to
with respect to ![]() belongs to the circle
belongs to the circle ![]() becouse
becouse ![]()
A circle ![]() containing points
containing points ![]() and
and ![]() symmetric with respect to
symmetric with respect to ![]() is orthogonal to
is orthogonal to ![]() (Claim 2) and maps into itself under inversion with respect to the circle
(Claim 2) and maps into itself under inversion with respect to the circle ![]() Hence, the point
Hence, the point ![]() under this inversion passes to some point
under this inversion passes to some point ![]() of the same circle
of the same circle ![]()
A straight line ![]() containing the point
containing the point ![]() of the circle
of the circle ![]() under inversion with respect to
under inversion with respect to ![]() maps into the circle
maps into the circle ![]() Hence, the inscribed angles of this circle are equal
Hence, the inscribed angles of this circle are equal ![]()
![]() maps into
maps into ![]() and
and ![]() maps into
maps into ![]() Consequently, the angles
Consequently, the angles ![]() These angles subtend the
These angles subtend the ![]() of the
of the ![]() circle, that is, the point
circle, that is, the point ![]() symmetric to the point
symmetric to the point ![]() with respect to
with respect to ![]() belongs to the circle
belongs to the circle ![]()
vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2018 IMO (Problems) • Resources | ||
| Preceded by Problem 5 |
1 • 2 • 3 • 4 • 5 • 6 | Followed by Last Problem |
| All IMO Problems and Solutions | ||