Difference between revisions of "2015 AIME I Problems/Problem 6"
(→See Also) |
(→Solution 3) |
||
| Line 78: | Line 78: | ||
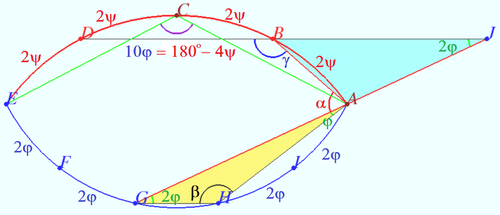
<cmath>BD||GH \implies \angle AJB = \angle AGH = 2 \varphi.</cmath> | <cmath>BD||GH \implies \angle AJB = \angle AGH = 2 \varphi.</cmath> | ||
| − | <cmath>\triangle AHG: \angle AHG = \beta = 180^\circ – 3 \varphi </cmath> | + | <cmath>\triangle AHG: \angle AHG = \beta = 180^\circ – 3 \varphi.</cmath> |
| − | <cmath>\triangle ABJ: | + | <cmath>\triangle ABJ: \angle BAG + \angle ABD = \alpha + \gamma = 180^\circ + 2 \varphi. </cmath> |
Let arc <math> \overset{\Large\frown} {AB} = 2\psi \implies</math> | Let arc <math> \overset{\Large\frown} {AB} = 2\psi \implies</math> | ||
| − | <math>\angle ACE = \frac {360^\circ – 8 \psi}{2}= 180^\circ – 4 \psi, \angle ABD = \frac {360^\circ – 6 \psi}{2} =180^\circ – 3 \psi.</math> | + | <math>\angle ACE = \frac {360^\circ – 8 \psi}{2}= 180^\circ – 4 \psi, \angle ABD = \gamma =\frac {360^\circ – 6 \psi}{2} =180^\circ – 3 \psi.</math> |
| − | <math>\ | + | <math>\gamma – \beta = 3(\varphi – \psi) = 12^\circ \implies \psi = \varphi – 4^\circ \implies 10 \varphi = 180^\circ – 4(\varphi – 4^\circ) \implies 14 \varphi = 168^\circ \implies \varphi = 12^\circ.</math> |
Therefore <math>\gamma = 180^\circ – 3 \cdot (12^\circ – 4^\circ) = 156^\circ \implies \alpha = 180^\circ + 2 \cdot 12^\circ – 156^\circ = \boxed{\textbf{058}}.</math> | Therefore <math>\gamma = 180^\circ – 3 \cdot (12^\circ – 4^\circ) = 156^\circ \implies \alpha = 180^\circ + 2 \cdot 12^\circ – 156^\circ = \boxed{\textbf{058}}.</math> | ||
Revision as of 13:50, 1 September 2022
Contents
[hide]Problem
Point ![]() and
and ![]() are equally spaced on a minor arc of a circle. Points
are equally spaced on a minor arc of a circle. Points ![]() and
and ![]() are equally spaced on a minor arc of a second circle with center
are equally spaced on a minor arc of a second circle with center ![]() as shown in the figure below. The angle
as shown in the figure below. The angle ![]() exceeds
exceeds ![]() by
by ![]() . Find the degree measure of
. Find the degree measure of ![]() .
.
![[asy] pair A,B,C,D,E,F,G,H,I,O; O=(0,0); C=dir(90); B=dir(70); A=dir(50); D=dir(110); E=dir(130); draw(arc(O,1,50,130)); real x=2*sin(20*pi/180); F=x*dir(228)+C; G=x*dir(256)+C; H=x*dir(284)+C; I=x*dir(312)+C; draw(arc(C,x,200,340)); label("$A$",A,dir(0)); label("$B$",B,dir(75)); label("$C$",C,dir(90)); label("$D$",D,dir(105)); label("$E$",E,dir(180)); label("$F$",F,dir(225)); label("$G$",G,dir(260)); label("$H$",H,dir(280)); label("$I$",I,dir(315)); [/asy]](http://latex.artofproblemsolving.com/5/5/9/5590bc90f068d76cce0399a7cf16b9bcf4f72c94.png)
Solution 1
Let ![]() be the center of the circle with
be the center of the circle with ![]() on it.
on it.
Let ![]() be the degree measurement of
be the degree measurement of ![]() in circle
in circle ![]()
and ![]() be the degree measurement of
be the degree measurement of ![]() in circle
in circle ![]() .
.
![]() is, therefore,
is, therefore, ![]() by way of circle
by way of circle ![]() and
and ![]() by way of circle
by way of circle ![]() .
.
![]() is
is ![]() by way of circle
by way of circle ![]() , and
, and ![]() by way of circle
by way of circle ![]() .
.
This means that:
![]()
which when simplified yields ![]() or
or ![]() Since:
Since:
![]() and
and ![]() So:
So:
![]()
![]()
![]() is equal to
is equal to ![]() +
+ ![]() , which equates to
, which equates to ![]() .
Plugging in yields
.
Plugging in yields ![]() , or
, or ![]() .
.
Solution 2
Let ![]() be the degree measurement of
be the degree measurement of ![]() . Since
. Since ![]() lie on a circle with center
lie on a circle with center ![]() ,
, ![]() .
.
Since ![]() ,
, ![]() . Adding
. Adding ![]() and
and ![]() gives
gives ![]() , and
, and ![]() . Since
. Since ![]() is parallel to
is parallel to ![]() ,
, ![]()
![]() .
.
We are given that ![]() are evenly distributed on a circle. Hence,
are evenly distributed on a circle. Hence,
![]()
![]()
Here comes the key: Draw a line through ![]() parallel to
parallel to ![]() , and select a point
, and select a point ![]() to the right of point
to the right of point ![]() .
.
![]() =
= ![]() +
+ ![]() =
= ![]() .
.
Let the midpoint of ![]() be
be ![]() , then
, then ![]() . Solving gives
. Solving gives ![]()
The rest of the solution proceeds as in solution 1, which gives ![]()
Solution 3
Let ![]()
![]()
![]()
![]()
![]()
![]() Let arc
Let arc ![]()
![]()
![]()
Therefore ![]()
See Also
| 2015 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.