Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2005 PMWC Problems/Problem T8"

(sol)
 
m (→‎Solution)
Line 5: Line 5:
 
[[Image:2005_PMWC-T8.png]]
 
[[Image:2005_PMWC-T8.png]]
  
−
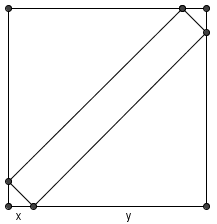
Since the figure in the middle is a rectangle, the isosceles triangles on opposite vertices are congruent. Let <math>x</math> be a leg of the first two, and <math>y</math> the other two. The sum of the areas of the triangle is then <math>2\left(\frac{1}{2}x^2\right) + 2\left(\frac{1}{2}y^2\right) = x^2 + y^2 = 200</math>. (remember that the sides are of unequal lengths, so we exclude <math>x = y=  10</math>). Since squares <math>\equiv 0,1 \pmod{4}</math>, we can reduce our search to even integers, and a short bit of trial and error yield <math>x = 2, y = 14</math> works.  
+
Since the figure in the middle is a rectangle, the isosceles triangles on opposite vertices are congruent. Let <math>x</math> be a leg of the first two, and <math>y</math> the other two. The sum of the areas of the triangle is then <math>2\left(\frac{1}{2}x^2\right) + 2\left(\frac{1}{2}y^2\right) = x^2 + y^2 = 200</math>. (Remember that the sides are of unequal lengths, so we exclude <math>x = y=  10</math>). Since squares <math>\equiv 0,1 \pmod{4}</math>, we can reduce our search to even integers, and a short bit of trial and error yield <math>x = 2, y = 14</math> works.  
  
 
Using subtraction of areas or 45-45-90 triangles, we find that the area of the rectangle is <math>(x + y)^2 - x^2 - y^2 = 2xy</math>; so the area of the rectangle is <math>2(2)(14) = 56</math>.
 
Using subtraction of areas or 45-45-90 triangles, we find that the area of the rectangle is <math>(x + y)^2 - x^2 - y^2 = 2xy</math>; so the area of the rectangle is <math>2(2)(14) = 56</math>.

Revision as of 11:11, 10 October 2007

Problem

An isosceles right triangle is removed from each corner of a square piece of paper so that a rectangle of unequal sides remains. If the sum of the areas of the cut-off pieces is and the lengths of the legs of the triangles cut off are integers, find the area of the rectangle.

Solution

2005 PMWC-T8.png

Since the figure in the middle is a rectangle, the isosceles triangles on opposite vertices are congruent. Let $x$ be a leg of the first two, and $y$ the other two. The sum of the areas of the triangle is then $2\left(\frac{1}{2}x^2\right) + 2\left(\frac{1}{2}y^2\right) = x^2 + y^2 = 200$. (Remember that the sides are of unequal lengths, so we exclude $x = y= 10$). Since squares $\equiv 0,1 \pmod{4}$, we can reduce our search to even integers, and a short bit of trial and error yield $x = 2, y = 14$ works.

Using subtraction of areas or 45-45-90 triangles, we find that the area of the rectangle is $(x + y)^2 - x^2 - y^2 = 2xy$; so the area of the rectangle is $2(2)(14) = 56$.

See also

2005 PMWC (Problems)
Preceded by
Problem T7 		Followed by
Problem T9
I: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
T: 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_PMWC_Problems/Problem_T8&oldid=17791"