Difference between revisions of "De Longchamps point"
(→de Longchamps point) |
(→See Also) |
||
| Line 75: | Line 75: | ||
<math>2\vec {HG} = \vec GL_o, 2\vec {GO} = \vec HG \implies L_o = L</math> as desired. | <math>2\vec {HG} = \vec GL_o, 2\vec {GO} = \vec HG \implies L_o = L</math> as desired. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==De Longchamps circle== | ||
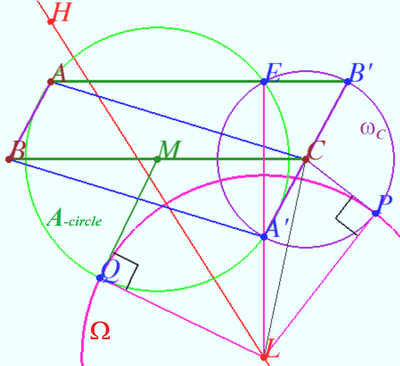
| + | [[File:Longchamps circle.png|400px|right]] | ||
| + | De Longchamps circle <math>\Omega</math> of the obtuse triangle <math>ABC</math> is circle centered at de Longchamps point <math>L</math> which is orthogonal to the <math>\omega_C.</math> Prove that de Longchamps circle is orthogonal to the <math>\omega_A, \omega_B, A-</math>power, <math>B-</math>power and <math>C-</math>power cicles and the radius of de Longchamps circle is <math>R_{\Omega} = 4R \sqrt { – \cos A \cos B \cos C}.</math> | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | <math>\vec {A'B'} = 2\vec {BA}, A'B'</math> – diameter <math>\omega_C.</math> | ||
| + | |||
| + | Let <math>E</math> be the foot of perpendicular from <math>L</math> to <math>AB'.</math> | ||
| + | |||
| + | Let <math>E_0</math> be crosspoint of <math>\omega_C</math> and <math>AB' \implies A'E_0 \perp AB' \implies E = E_0.</math> | ||
| + | |||
| + | Points <math>A'</math> and <math>E</math> are simmetric with respect to <math>BC, MA' = AM \implies</math> | ||
| + | |||
| + | Points <math>A'</math> and <math>E</math> lies on <math>A-</math>power circle and on <math>\omega_C</math>. | ||
| + | |||
| + | <math>\Omega \perp \omega_C,</math> points <math>L, A',</math> and <math>E</math> are collinear <math>\implies \Omega \perp A-</math> power circle. | ||
| + | |||
| + | <math>L</math> is the radical center of all six circles, therefore <math>\Omega</math> is perpendicular to each of these circles. | ||
| + | <math>L</math> is orthocenter of the anticomplementary triangle of <math>\triangle ABC</math> so radius of <math>\Omega</math> is twice radius of circle finded by Claim <math>\implies R_{\Omega} = 4R \sqrt { – \cos A \cos B \cos C}.</math> | ||
| + | |||
| + | <i><b>Claim (Radius)</b></i> | ||
| + | |||
| + | Let <math>ABC</math> be obtuse triangle <math>(\angle A > 90^\circ)</math> with circumcircle <math>\Omega,</math> circumradius <math>R,</math> and orthocenter <math>H.</math> | ||
| + | Let <math>\omega'</math> be the circle with diameter <math>AB.</math> | ||
| + | Let <math>\omega</math> be the circle perpendicular to <math>\omega'</math> centered at <math>H.</math> Find <math>R_\omega,</math> the radius of <math>\omega.</math> | ||
| + | |||
| + | Let altitude <math>AH</math> cross <math>BC</math> at <math>D</math> and cross <math>\Omega</math> second time at <math>H'.</math> | ||
| + | <math>AD \perp BD \implies D \in \omega',</math> points <math>H,A, D</math> are collinear <math>\implies</math> inversion with respect <math>\omega</math> swap <math>A</math> and <math>D \implies R_\omega^2 = HA \cdot HD.</math> | ||
| + | Well known that <math>HA = – 2R \cos A.</math> | ||
| + | <cmath>BC \perp HD, AC \perp BH \implies \angle C = \angle BHD \implies HD = BH \cos C.</cmath> | ||
| + | Points <math>H</math> and <math>H'</math> are symmetric with respect <math>BC \implies BH' = BH.</math> | ||
| + | <cmath>\angle BAH' = 90^\circ – \angle B \implies BH' = 2R \sin \angle BAH' = 2R \cos B \implies</cmath> | ||
| + | <cmath>R_\omega^2 = – 2R \cos A \cdot 2R \cos B \cos C \implies R_\omega = 2R \sqrt{– \cos A \cos B \cos C}.</cmath> | ||
| + | |||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 07:53, 16 November 2022
- The title of this article has been capitalized due to technical restrictions. The correct title should be de Longchamps point.
|
|
| The de Longchamps point ( orthocenter ( through the circumcenter ( |
The de Longchamps point of a triangle is the reflection of the triangle's orthocenter through its circumcenter.
The point is collinear with the orthocenter and circumcenter.
de Longchamps point
Definition 1
The de Longchamps point of a triangle is the radical center of the power circles of the triangle. Prove that De Longchamps point lies on Euler line.
We call A-power circle of a ![]() the circle centered at the midpoint
the circle centered at the midpoint ![]() point
point ![]() with radius
with radius ![]() The other two circles are defined symmetrically.
The other two circles are defined symmetrically.
Proof
Let ![]() and
and ![]() be orthocenter, circumcenter, and De Longchamps point, respectively.
be orthocenter, circumcenter, and De Longchamps point, respectively.
Denote ![]() power circle by
power circle by ![]() power circle by
power circle by ![]()
![]() WLOG,
WLOG, ![]()
Denote ![]() the projection of point
the projection of point ![]() on
on ![]()
We will prove that radical axes of ![]() power and
power and ![]() power cicles is symmetric to altitude
power cicles is symmetric to altitude ![]() with respect
with respect ![]() Further, we will conclude that the point of intersection of the radical axes, symmetrical to the heights with respect to O, is symmetrical to the point of intersection of the heights
Further, we will conclude that the point of intersection of the radical axes, symmetrical to the heights with respect to O, is symmetrical to the point of intersection of the heights ![]() with respect to
with respect to ![]()
Point ![]() is the crosspoint of the center line of the
is the crosspoint of the center line of the ![]() power and
power and ![]() power circles and there radical axis.
power circles and there radical axis. ![]() We use claim and get:
We use claim and get:
![]()
![]() and
and ![]() are the medians, so
are the medians, so
![]()
We use Claim some times and get:
![]()
![]() radical axes of
radical axes of ![]() power and
power and ![]() power cicles is symmetric to altitude
power cicles is symmetric to altitude ![]() with respect
with respect ![]()
Similarly radical axes of ![]() power and
power and ![]() power cicles is symmetric to altitude
power cicles is symmetric to altitude ![]() radical axes of
radical axes of ![]() power and
power and ![]() power cicles is symmetric to altitude
power cicles is symmetric to altitude ![]() with respect
with respect ![]() Therefore the point
Therefore the point ![]() of intersection of the radical axes, symmetrical to the heights with respect to
of intersection of the radical axes, symmetrical to the heights with respect to ![]() is symmetrical to the point
is symmetrical to the point ![]() of intersection of the heights with respect to
of intersection of the heights with respect to ![]() lies on Euler line of
lies on Euler line of ![]()
Claim (Distance between projections)
![]()
![]()
![]()
Definition 2
We call ![]() circle of a
circle of a ![]() the circle centered at
the circle centered at ![]() with radius
with radius ![]() The other two circles are defined symmetrically. The De Longchamps point of a triangle is the radical center of
The other two circles are defined symmetrically. The De Longchamps point of a triangle is the radical center of ![]() circle,
circle, ![]() circle, and
circle, and ![]() circle of the triangle (Casey – 1886). Prove that De Longchamps point under this definition is the same as point under Definition 1.
circle of the triangle (Casey – 1886). Prove that De Longchamps point under this definition is the same as point under Definition 1.
Proof
Let ![]() and
and ![]() be orthocenter, centroid, and De Longchamps point, respectively. Let
be orthocenter, centroid, and De Longchamps point, respectively. Let ![]() cross
cross ![]() at points
at points ![]() and
and ![]() The other points
The other points ![]() are defined symmetrically.
are defined symmetrically.
![]()
![]() Similarly
Similarly ![]() is diameter
is diameter ![]()
![]()
Therefore ![]() is anticomplementary triangle of
is anticomplementary triangle of ![]() is orthic triangle of
is orthic triangle of ![]() So
So ![]() is orthocenter of
is orthocenter of ![]()
![]() as desired.
as desired.
vladimir.shelomovskii@gmail.com, vvsss
De Longchamps circle
De Longchamps circle ![]() of the obtuse triangle
of the obtuse triangle ![]() is circle centered at de Longchamps point
is circle centered at de Longchamps point ![]() which is orthogonal to the
which is orthogonal to the ![]() Prove that de Longchamps circle is orthogonal to the
Prove that de Longchamps circle is orthogonal to the ![]() power,
power, ![]() power and
power and ![]() power cicles and the radius of de Longchamps circle is
power cicles and the radius of de Longchamps circle is ![]()
Proof
![]() – diameter
– diameter ![]()
Let ![]() be the foot of perpendicular from
be the foot of perpendicular from ![]() to
to ![]()
Let ![]() be crosspoint of
be crosspoint of ![]() and
and ![]()
Points ![]() and
and ![]() are simmetric with respect to
are simmetric with respect to ![]()
Points ![]() and
and ![]() lies on
lies on ![]() power circle and on
power circle and on ![]() .
.
![]() points
points ![]() and
and ![]() are collinear
are collinear ![]() power circle.
power circle.
![]() is the radical center of all six circles, therefore
is the radical center of all six circles, therefore ![]() is perpendicular to each of these circles.
is perpendicular to each of these circles.
![]() is orthocenter of the anticomplementary triangle of
is orthocenter of the anticomplementary triangle of ![]() so radius of
so radius of ![]() is twice radius of circle finded by Claim
is twice radius of circle finded by Claim ![]()
Claim (Radius)
Let ![]() be obtuse triangle
be obtuse triangle ![]() with circumcircle
with circumcircle ![]() circumradius
circumradius ![]() and orthocenter
and orthocenter ![]() Let
Let ![]() be the circle with diameter
be the circle with diameter ![]() Let
Let ![]() be the circle perpendicular to
be the circle perpendicular to ![]() centered at
centered at ![]() Find
Find ![]() the radius of
the radius of ![]()
Let altitude ![]() cross
cross ![]() at
at ![]() and cross
and cross ![]() second time at
second time at ![]()
![]() points
points ![]() are collinear
are collinear ![]() inversion with respect
inversion with respect ![]() swap
swap ![]() and
and ![]() Well known that
Well known that ![]()
![]() Points
Points ![]() and
and ![]() are symmetric with respect
are symmetric with respect ![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
See Also
This article is a stub. Help us out by expanding it.





![[asy] draw((0,0)--(44,60)--(44,-10)--cycle); draw((0,0)--(44,0),blue+dashed); draw((44,60)--(22,-5),blue+dashed); draw((44,-10)--(6.5,10),blue+dashed); label("H",(24,0),(1,1)); dot((24,0)); draw((22,30)--(44,14),red); draw((22,-5)--(34,46),red); draw((44,25)--(18,25),red); dot((29,25)); label("C",(29,25),(1,1)); draw(Circle((29,25),25),dashed); dot((34,50)); label("L",(34,50),(1,1)); [/asy]](http://latex.artofproblemsolving.com/8/e/2/8e2fc3535addbb951f5f9621f4305542f0734745.png)