Difference between revisions of "2014 AMC 12B Problems/Problem 24"
Isabelchen (talk | contribs) m (→Solution 4) |
Isabelchen (talk | contribs) (→Solution 4) |
||
| Line 143: | Line 143: | ||
Let <math>BE = a</math>, <math>AC = CE = BD = b</math> | Let <math>BE = a</math>, <math>AC = CE = BD = b</math> | ||
| − | By [[Ptolemy's theorem]] for quadrilateral <math>ABCE</math>, <math>3c + 140 = ab</math>, <math>a = 3 + \frac{140}{b}</math> | + | By [[Ptolemy's theorem]] for quadrilateral <math>ABCE</math>, <math>AB \cdot DE + BC \cdot AE = BC \cdot AC</math>, <math>3c + 140 = ab</math>, <math>a = 3 + \frac{140}{b}</math> |
| − | By [[Ptolemy's theorem]] for quadrilateral <math> | + | By [[Ptolemy's theorem]] for quadrilateral <math>BCDE</math>, <math>CD \cdot BE + BC \cdot DE = BD \cdot CE</math>, <math>3a + 100 = b^2</math> |
<math>3(3 + \frac{140}{b}) + 100 = b^2</math>, <math>b^3 - 109 b -420 = 0</math>, <math>(b-12)(b+7)(b+5) = 0</math>, <math>b = 12</math> | <math>3(3 + \frac{140}{b}) + 100 = b^2</math>, <math>b^3 - 109 b -420 = 0</math>, <math>(b-12)(b+7)(b+5) = 0</math>, <math>b = 12</math> | ||
| Line 151: | Line 151: | ||
<math>a = 3 + \frac{140}{12} = \frac{44}{3}</math> | <math>a = 3 + \frac{140}{12} = \frac{44}{3}</math> | ||
| − | By [[Ptolemy's theorem]] for quadrilateral <math>ABDE</math>, <math>AD \cdot a = 14b + 30</math>, <math>AD = \frac{27}{2}</math> | + | By [[Ptolemy's theorem]] for quadrilateral <math>ABDE</math>, <math>AE \cdot BD + AB \cdot DE = AD \cdot BE</math>, <math>AD \cdot a = 14b + 30</math>, <math>AD = \frac{27}{2}</math> |
<math>12 + 12 + 12 + \frac{44}{3} + \frac{27}{2} = \boxed{\textbf{(D) }391}</math> | <math>12 + 12 + 12 + \frac{44}{3} + \frac{27}{2} = \boxed{\textbf{(D) }391}</math> | ||
Revision as of 07:00, 1 January 2023
Contents
[hide]Problem
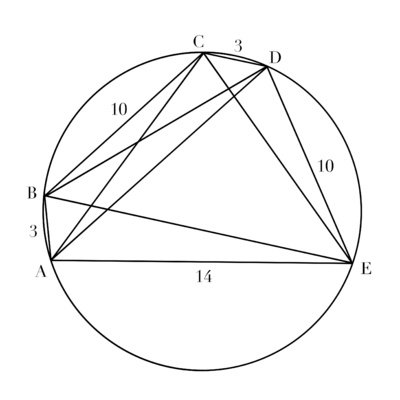
Let ![]() be a pentagon inscribed in a circle such that
be a pentagon inscribed in a circle such that ![]() ,
, ![]() , and
, and ![]() . The sum of the lengths of all diagonals of
. The sum of the lengths of all diagonals of ![]() is equal to
is equal to ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. What is
are relatively prime positive integers. What is ![]() ?
?
![]()
Video Solution by Punxsutawney Phil
https://www.youtube.com/watch?v=1-2vT_GIceA
Solution 1
Let ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() be on
be on ![]() such that
such that ![]() .
.
![[asy] size(200); defaultpen(linewidth(0.4)+fontsize(10)); pen s = linewidth(0.8)+fontsize(8); pair O,A,B,C,D,E0,F; O=origin; A= dir(198); path c = CR(O,1); real r = 0.13535; B = IP(c, CR(A,3*r)); C = IP(c, CR(B,10*r)); D = IP(c, CR(C,3*r)); E0 = OP(c, CR(D,10*r)); F = foot(C,A,E0); dot("$A$", A, A-O); dot("$B$", B, B-O); dot("$C$", C, C-O); dot("$D$", D, D-O); dot("$E$", E0, E0-O); dot("$F$", F, F-C); label("$c$",A--C,S); label("$c$",E0--C,W); label("$7$",F--E0,S); label("$7$",F--A,S); label("$3$",A--B,2*W); label("$10$",B--C,2*N); label("$3$",C--D,2*NE); label("$10$",D--E0,E); draw(A--B--C--D--E0--A, black+0.8); draw(CR(O,1), s); draw(A--C--E0, royalblue); draw(C--F, royalblue+dashed); draw(rightanglemark(E0,F,C,2)); MA("\theta",A,B,C,0.075); MA("\pi-\theta",C,E0,A,0.1); [/asy]](http://latex.artofproblemsolving.com/f/3/0/f309928844b6dc47e0410382e86dd44b9cf39966.png) In
In ![]() we have
we have ![]() . We use the Law of Cosines on
. We use the Law of Cosines on ![]() to get
to get ![]() . Eliminating
. Eliminating ![]() we get
we get ![]() which factorizes as
which factorizes as
![]() Discarding the negative roots we have
Discarding the negative roots we have ![]() . Thus
. Thus ![]() . For
. For ![]() , we use Ptolemy's theorem on cyclic quadrilateral
, we use Ptolemy's theorem on cyclic quadrilateral ![]() to get
to get ![]() . For
. For ![]() , we use Ptolemy's theorem on cyclic quadrilateral
, we use Ptolemy's theorem on cyclic quadrilateral ![]() to get
to get ![]() .
.
The sum of the lengths of the diagonals is ![]() so the answer is
so the answer is ![]()
Solution 2
Let ![]() denote the length of a diagonal opposite adjacent sides of length
denote the length of a diagonal opposite adjacent sides of length ![]() and
and ![]() ,
, ![]() for sides
for sides ![]() and
and ![]() , and
, and ![]() for sides
for sides ![]() and
and ![]() . Using Ptolemy's Theorem on the five possible quadrilaterals in the configuration, we obtain:
. Using Ptolemy's Theorem on the five possible quadrilaterals in the configuration, we obtain:

Using equations ![]() and
and ![]() , we obtain:
, we obtain:
![]()
and
![]()
Plugging into equation ![]() , we find that:
, we find that:

Or similarly into equation ![]() to check:
to check:

![]() , being a length, must be positive, implying that
, being a length, must be positive, implying that ![]() . In fact, this is reasonable, since
. In fact, this is reasonable, since ![]() in the pentagon with apparently obtuse angles. Plugging this back into equations
in the pentagon with apparently obtuse angles. Plugging this back into equations ![]() and
and ![]() we find that
we find that ![]() and
and ![]() .
.
We desire ![]() , so it follows that the answer is
, so it follows that the answer is ![]()
Solution 3 (Ptolemy's but Quicker)
Let us set ![]() to be
to be ![]() and
and ![]() to be
to be ![]() and
and ![]() to be
to be ![]() . It follow from applying Ptolemy's Theorem on
. It follow from applying Ptolemy's Theorem on ![]() to get
to get ![]() . Applying Ptolemy's on
. Applying Ptolemy's on ![]() gives
gives ![]() ; and applying Ptolemy's on
; and applying Ptolemy's on ![]() gives
gives ![]() . So, we have the have the following system of equations:
. So, we have the have the following system of equations:

From ![]() , we have
, we have ![]() . Isolating the x gives
. Isolating the x gives ![]() . By setting
. By setting ![]() and
and ![]() equal, we have
equal, we have ![]() . Manipulating it gives
. Manipulating it gives ![]() . Finally, plugging back into
. Finally, plugging back into ![]() gives
gives ![]() . Plugging in the
. Plugging in the ![]() as well gives
as well gives

It is impossible for ![]() for
for ![]() ; that means
; that means ![]() . That means
. That means ![]() and
and ![]() .
.
Thus, the sum of all diagonals is ![]() , which implies our answer is
, which implies our answer is ![]() .
.
~sml1809
Solution 4
Let ![]() ,
, ![]()
By Ptolemy's theorem for quadrilateral ![]() ,
, ![]() ,
, ![]() ,
, ![]()
By Ptolemy's theorem for quadrilateral ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
By Ptolemy's theorem for quadrilateral ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
See also
| 2014 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 23 |
Followed by Problem 25 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()