Difference between revisions of "2015 AIME I Problems/Problem 11"
m |
m |
||
| (13 intermediate revisions by 7 users not shown) | |||
| Line 2: | Line 2: | ||
Triangle <math>ABC</math> has positive integer side lengths with <math>AB=AC</math>. Let <math>I</math> be the intersection of the bisectors of <math>\angle B</math> and <math>\angle C</math>. Suppose <math>BI=8</math>. Find the smallest possible perimeter of <math>\triangle ABC</math>. | Triangle <math>ABC</math> has positive integer side lengths with <math>AB=AC</math>. Let <math>I</math> be the intersection of the bisectors of <math>\angle B</math> and <math>\angle C</math>. Suppose <math>BI=8</math>. Find the smallest possible perimeter of <math>\triangle ABC</math>. | ||
| − | ==Solution 1 | + | ==Solution 1== |
| − | |||
| − | |||
| − | |||
| − | |||
Let <math>D</math> be the midpoint of <math>\overline{BC}</math>. Then by SAS Congruence, <math>\triangle ABD \cong \triangle ACD</math>, so <math>\angle ADB = \angle ADC = 90^o</math>. | Let <math>D</math> be the midpoint of <math>\overline{BC}</math>. Then by SAS Congruence, <math>\triangle ABD \cong \triangle ACD</math>, so <math>\angle ADB = \angle ADC = 90^o</math>. | ||
| Line 27: | Line 23: | ||
Thus the perimeter of <math>\triangle ABC</math> must be <math>2(x+y) = \boxed{108}</math>. | Thus the perimeter of <math>\triangle ABC</math> must be <math>2(x+y) = \boxed{108}</math>. | ||
| + | |||
| + | ==Solution 2 (No Trig)== | ||
| + | Let <math>AB=x</math> and the foot of the altitude from <math>A</math> to <math>BC</math> be point <math>E</math> and <math>BE=y</math>. Since ABC is isosceles, <math>I</math> is on <math>AE</math>. By Pythagorean Theorem, <math>AE=\sqrt{x^2-y^2}</math>. Let <math>IE=a</math> and <math>IA=b</math>. By Angle Bisector theorem, <math>\frac{y}{a}=\frac{x}{b}</math>. Also, <math>a+b=\sqrt{x^2-y^2}</math>. Solving for <math>a</math>, we get <math>a=\frac{\sqrt{x^2-y^2}}{1+\frac{x}{y}}</math>. Then, using Pythagorean Theorem on <math>\triangle BEI</math> we have <math>y^2+\left(\frac{\sqrt{x^2-y^2}}{1+\frac{x}{y}}\right)^2=8^2=64</math>. Simplifying, we have <math>y^2+y^2\frac{x^2-y^2}{(x+y)^2}=64</math>. Factoring out the <math>y^2</math>, we have <math>y^2\left(1+\frac{x^2-y^2}{(x+y)^2}\right)=64</math>. Adding 1 to the fraction and simplifying, we have <math>\frac{y^2x(x+y)}{(x+y)^2}=32</math>. Crossing out the <math>x+y</math>, and solving for <math>x</math> yields <math>32y = x(y^2-32)</math>. Then, we continue as Solution 1 does. | ||
| + | |||
| + | ==Solution 3== | ||
| + | Let <math>AB=x</math>, call the midpoint of <math>BC</math> point <math>E</math>, call the point where the incircle meets <math>AB</math> point <math>D</math>, | ||
| + | |||
| + | and let <math>BE=y</math>. We are looking for the minimum value of <math>2(x+y)</math>. <math>AE</math> is an altitude because the triangle | ||
| + | |||
| + | is isosceles. By Pythagoras on <math>BEI</math>, the inradius is <math>\sqrt{64-y^2}</math> and by Pythagoras on <math>ABE</math>, <math>AE</math> is | ||
| + | |||
| + | <math>\sqrt{x^2-y^2}</math>. By equal tangents, <math>BE=BD=y</math>, so <math>AD=x-y</math>. Since <math>ID</math> is an inradius, <math>ID=IE</math> and | ||
| + | using pythagoras on <math>ADI</math> yields <math>AI=</math><math>\sqrt{x^2-2xy+64}</math>. <math>ADI</math> is similar to <math>AEB</math> by <math>AA</math>, so we | ||
| + | |||
| + | can write <math>\frac{x-y}{\sqrt{x^2-2xy+64}}=\frac{\sqrt{x^2-y^2}}{x}</math>. Simplifying, <math>\frac{x}{\sqrt{x^2-2xy+64}}=\sqrt{\frac{x+y}{x-y}}</math>. | ||
| + | |||
| + | Squaring, subtracting 1 from both sides, and multiplying everything out, we get <math>yx^2-2xy^2+64y=yx^2 -32x+32y-xy^2</math>, which turns into <math>32y=x(y^2-32)</math>. Finish as in Solution 1. | ||
| + | ==Solution 4== | ||
| + | Angle bisectors motivate trig bash. | ||
| + | Define angle <math>IBC = x</math>. Foot of perpendicular from <math>I</math> to <math>BC</math> is point <math>P</math>. | ||
| + | <math>\overline{BC} = 2\overline{BP} = 2(8\cos(x)) = N</math>, where <math>N</math> is an integer. Thus, <math>\cos(x) = \frac{N}{16}</math>. Via double angle, we calculate <math>\overline{AB}</math> to be <math>\frac{8\cos(x)}{2\cos(x)^2 - 1} = \frac{64N}{N^2 - 128}</math>. This is to be an integer. We can bound <math>N</math> now, as <math>N > 11</math> to avoid negative values and <math>N < 16</math> due to triangle inequality. Testing, <math>N = 12</math> works, giving <math>\overline{AB} = 48, \overline{BC} = 12</math>. | ||
| + | Our answer is <math>2 * 48 + 12 = \boxed{108}</math>. | ||
| + | - whatRthose | ||
| + | |||
| + | ==Solution 5== | ||
| + | |||
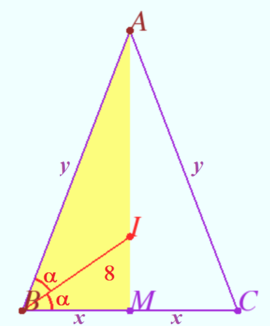
| + | [[File:2015 AIME I 11.png|270px|right]] | ||
| + | Let <math>M</math> be midpoint <math>BC, BM = x, AB = y, \angle IBM = \alpha.</math> | ||
| + | |||
| + | <math>BI</math> is the bisector of <math>\angle ABM</math> in <math>\triangle ABM.</math> | ||
| + | <math>BI = \frac {2 xy \cos \alpha}{x+y} = 8, \cos \alpha = \frac {x}{8} \implies \frac {x^2 y}{x+y} = 32.</math> | ||
| + | <cmath>y = \frac {32 x} {x^2 - 32}.</cmath> | ||
| + | <math>BC = 2x</math> is integer, <math>5.5^2 < 32 \implies x \ge 6.</math> | ||
| + | <math>BM < BI \implies x =\{ 6, 6.5, 7, 7.5 \}.</math> | ||
| + | |||
| + | If <math>x > 6</math> then <math>y</math> is not integer. | ||
| + | <cmath>x = 6 \implies y = 48 \implies 2(x+y) = \boxed{\textbf{108}}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ==Video Solution== | ||
| + | |||
| + | https://youtu.be/R8kvayz7Rtw?si=hFg4yGZO4dxyxAuG | ||
| + | |||
| + | ~MathProblemSolvingSkills.com | ||
| + | |||
==See Also== | ==See Also== | ||
Latest revision as of 17:43, 27 September 2023
Contents
[hide]Problem
Triangle ![]() has positive integer side lengths with
has positive integer side lengths with ![]() . Let
. Let ![]() be the intersection of the bisectors of
be the intersection of the bisectors of ![]() and
and ![]() . Suppose
. Suppose ![]() . Find the smallest possible perimeter of
. Find the smallest possible perimeter of ![]() .
.
Solution 1
Let ![]() be the midpoint of
be the midpoint of ![]() . Then by SAS Congruence,
. Then by SAS Congruence, ![]() , so
, so ![]() .
.
Now let ![]() ,
, ![]() , and
, and ![]() .
.
Then ![]()
and ![]() .
.
Cross-multiplying yields ![]() .
.
Since ![]() ,
, ![]() must be positive, so
must be positive, so ![]() .
.
Additionally, since ![]() has hypotenuse
has hypotenuse ![]() of length
of length ![]() ,
, ![]() .
.
Therefore, given that ![]() is an integer, the only possible values for
is an integer, the only possible values for ![]() are
are ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
However, only one of these values, ![]() , yields an integral value for
, yields an integral value for ![]() , so we conclude that
, so we conclude that ![]() and
and ![]() .
.
Thus the perimeter of ![]() must be
must be ![]() .
.
Solution 2 (No Trig)
Let ![]() and the foot of the altitude from
and the foot of the altitude from ![]() to
to ![]() be point
be point ![]() and
and ![]() . Since ABC is isosceles,
. Since ABC is isosceles, ![]() is on
is on ![]() . By Pythagorean Theorem,
. By Pythagorean Theorem, ![]() . Let
. Let ![]() and
and ![]() . By Angle Bisector theorem,
. By Angle Bisector theorem, ![]() . Also,
. Also, ![]() . Solving for
. Solving for ![]() , we get
, we get ![]() . Then, using Pythagorean Theorem on
. Then, using Pythagorean Theorem on ![]() we have
we have  . Simplifying, we have
. Simplifying, we have ![]() . Factoring out the
. Factoring out the ![]() , we have
, we have ![]() . Adding 1 to the fraction and simplifying, we have
. Adding 1 to the fraction and simplifying, we have ![]() . Crossing out the
. Crossing out the ![]() , and solving for
, and solving for ![]() yields
yields ![]() . Then, we continue as Solution 1 does.
. Then, we continue as Solution 1 does.
Solution 3
Let ![]() , call the midpoint of
, call the midpoint of ![]() point
point ![]() , call the point where the incircle meets
, call the point where the incircle meets ![]() point
point ![]() ,
,
and let ![]() . We are looking for the minimum value of
. We are looking for the minimum value of ![]() .
. ![]() is an altitude because the triangle
is an altitude because the triangle
is isosceles. By Pythagoras on ![]() , the inradius is
, the inradius is ![]() and by Pythagoras on
and by Pythagoras on ![]() ,
, ![]() is
is
![]() . By equal tangents,
. By equal tangents, ![]() , so
, so ![]() . Since
. Since ![]() is an inradius,
is an inradius, ![]() and
using pythagoras on
and
using pythagoras on ![]() yields
yields ![]()
![]() .
. ![]() is similar to
is similar to ![]() by
by ![]() , so we
, so we
can write ![]() . Simplifying,
. Simplifying, ![]() .
.
Squaring, subtracting 1 from both sides, and multiplying everything out, we get ![]() , which turns into
, which turns into ![]() . Finish as in Solution 1.
. Finish as in Solution 1.
Solution 4
Angle bisectors motivate trig bash.
Define angle ![]() . Foot of perpendicular from
. Foot of perpendicular from ![]() to
to ![]() is point
is point ![]() .
.
![]() , where
, where ![]() is an integer. Thus,
is an integer. Thus, ![]() . Via double angle, we calculate
. Via double angle, we calculate ![]() to be
to be ![]() . This is to be an integer. We can bound
. This is to be an integer. We can bound ![]() now, as
now, as ![]() to avoid negative values and
to avoid negative values and ![]() due to triangle inequality. Testing,
due to triangle inequality. Testing, ![]() works, giving
works, giving ![]() .
Our answer is
.
Our answer is ![]() .
- whatRthose
.
- whatRthose
Solution 5
Let ![]() be midpoint
be midpoint ![]()
![]() is the bisector of
is the bisector of ![]() in
in ![]()
![]()
![]()
![]() is integer,
is integer, ![]()
![]()
If ![]() then
then ![]() is not integer.
is not integer.
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
https://youtu.be/R8kvayz7Rtw?si=hFg4yGZO4dxyxAuG
~MathProblemSolvingSkills.com
See Also
| 2015 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 10 |
Followed by Problem 12 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()