Difference between revisions of "1988 AIME Problems/Problem 7"
m (Fixed some spelling and grammar) |
(→Solution) |
||
| Line 4: | Line 4: | ||
== Solution == | == Solution == | ||
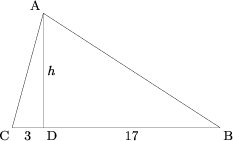
<center>[[Image:AIME_1988_Solution_07.png]]</center> | <center>[[Image:AIME_1988_Solution_07.png]]</center> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== See also == | == See also == | ||
Revision as of 19:12, 15 November 2023
Problem
In triangle ![]() ,
, ![]() , and the altitude from
, and the altitude from ![]() divides
divides ![]() into segments of length 3 and 17. What is the area of triangle
into segments of length 3 and 17. What is the area of triangle ![]() ?
?
Solution
See also
| 1988 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 6 |
Followed by Problem 8 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()









