Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2019 IMO Problems/Problem 2"

(→‎Solution)
 
Line 1: Line 1:
 +
==Problem==
 +
 
In triangle <math>ABC</math>, point <math>A_1</math> lies on side <math>BC</math> and point <math>B_1</math> lies on side <math>AC</math>. Let <math>P</math> and <math>Q</math> be points on segments <math>AA_1</math> and <math>BB_1</math>, respectively, such that <math>PQ</math> is parallel to <math>AB</math>. Let <math>P_1</math> be a point on line <math>PB_1</math>, such that <math>B_1</math> lies strictly between <math>P</math> and <math>P_1</math>, and <math>\angle PP_1C=\angle BAC</math>. Similarly, let <math>Q_1</math> be the point on line <math>QA_1</math>, such that <math>A_1</math> lies strictly between <math>Q</math> and <math>Q_1</math>, and <math>\angle CQ_1Q=\angle CBA</math>.
 
In triangle <math>ABC</math>, point <math>A_1</math> lies on side <math>BC</math> and point <math>B_1</math> lies on side <math>AC</math>. Let <math>P</math> and <math>Q</math> be points on segments <math>AA_1</math> and <math>BB_1</math>, respectively, such that <math>PQ</math> is parallel to <math>AB</math>. Let <math>P_1</math> be a point on line <math>PB_1</math>, such that <math>B_1</math> lies strictly between <math>P</math> and <math>P_1</math>, and <math>\angle PP_1C=\angle BAC</math>. Similarly, let <math>Q_1</math> be the point on line <math>QA_1</math>, such that <math>A_1</math> lies strictly between <math>Q</math> and <math>Q_1</math>, and <math>\angle CQ_1Q=\angle CBA</math>.
  
Line 33: Line 35:
  
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
==See Also==
 +
 +
{{IMO box|year=2019|num-b=1|num-a=3}}

Latest revision as of 00:49, 19 November 2023

Problem

In triangle $ABC$, point $A_1$ lies on side $BC$ and point $B_1$ lies on side $AC$. Let $P$ and $Q$ be points on segments $AA_1$ and $BB_1$, respectively, such that $PQ$ is parallel to $AB$. Let $P_1$ be a point on line $PB_1$, such that $B_1$ lies strictly between $P$ and $P_1$, and $\angle PP_1C=\angle BAC$. Similarly, let $Q_1$ be the point on line $QA_1$, such that $A_1$ lies strictly between $Q$ and $Q_1$, and $\angle CQ_1Q=\angle CBA$.

Prove that points $P,Q,P_1$, and $Q_1$ are concyclic.

Solution

2019 IMO 2.png
2019 IMO 2a.png

The essence of the proof is to build a circle through the points $P, Q,$ and two additional points $A_0$ and $B_0,$ then we prove that the points $P_1$ and $Q_1$ lie on the same circle.

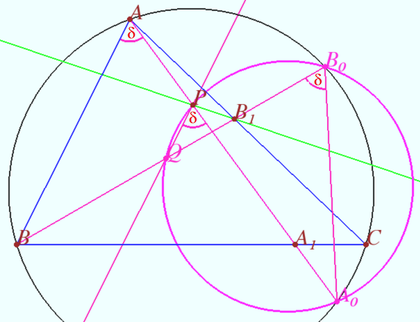
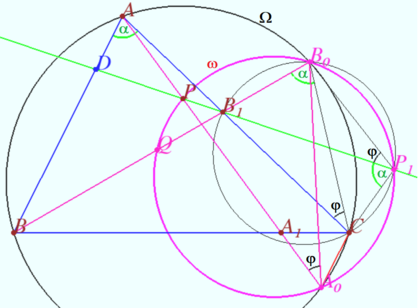
We assume that the intersection point of $AP$ and $BQ$ lies on the segment $PA_1.$ If it lies on segment $AP,$ then the proof is the same, but some angles will be replaced with additional ones up to $180^\circ$.

Let the circumcircle of $\triangle ABC$ be $\Omega$. Let $A_0$ and $B_0$ be the points of intersection of $AP$ and $BQ$ with $\Omega$. Let $\angle BAP = \delta.$

\[PQ||AB \implies \angle QPA_0 = \delta.\]

$\angle BAP = \angle BB_0A_0 = \delta$ since they intersept the arc $BA_0$ of the circle $\Omega$.

$\angle QPA_0 = \angle QB_0A_0 \implies QPB_0A_0$ is cyclic (in circle $\omega.$)

Let $\angle BAC = \alpha, \angle AA_0B_0 = \varphi.$

$\angle PP_1C = \alpha, \angle BB_0C = \alpha$ since they intersept the arc $BC$ of the circle $\Omega.$ So $B_0P_1CB_1$ is cyclic.

$\angle ACB_0 = \angle AA_0B_0 = \varphi$ (they intersept the arc $A_0B_0$ of the circle $\Omega).$

$\angle B_1CB_0 = \varphi.$ $\angle B_1P_1B_0 = \angle B_1CB_0 = \varphi$ (since they intersept the arc $B_1B_0$ of the circle $B_0P_1CB_1).$

Hence $\angle PA_0B_0 = \angle PP_1B_0 = \varphi,$ the point $P_1$ lies on $\omega.$

Similarly, point $Q_1$ lies on $\omega.$

vladimir.shelomovskii@gmail.com, vvsss

See Also

2019 IMO (Problems) • Resources
Preceded by
Problem 1 		1 • 2 • 3 • 4 • 5 • 6 Followed by
Problem 3
All IMO Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2019_IMO_Problems/Problem_2&oldid=204591"