Difference between revisions of "Polya’s method for extremums"
(Created page with "==The segment of the shortest length== The segment <math>AB</math> has the ends on the sides of a right angle and contains a point <math>C(x_C, y_C).</math> Find the shortest...") |
(→The segment of the shortest length) |
||
| Line 1: | Line 1: | ||
==The segment of the shortest length== | ==The segment of the shortest length== | ||
| + | [[File:Shortest segment.png|400px|right]] | ||
The segment <math>AB</math> has the ends on the sides of a right angle and contains a point <math>C(x_C, y_C).</math> Find the shortest length of such a segment. | The segment <math>AB</math> has the ends on the sides of a right angle and contains a point <math>C(x_C, y_C).</math> Find the shortest length of such a segment. | ||
| + | |||
<i><b>Solution</b></i> | <i><b>Solution</b></i> | ||
Let's imagine that <math>AB</math> is a spring rod that cannot bend, but tends to shorten its length. | Let's imagine that <math>AB</math> is a spring rod that cannot bend, but tends to shorten its length. | ||
| + | |||
The rod is fixed at point <math>C</math> on a hinge without friction. The hinge allows the rod to rotate and slide. | The rod is fixed at point <math>C</math> on a hinge without friction. The hinge allows the rod to rotate and slide. | ||
| + | |||
The ends of the rod can slide without friction along the grooves - the sides of the corner. | The ends of the rod can slide without friction along the grooves - the sides of the corner. | ||
| + | |||
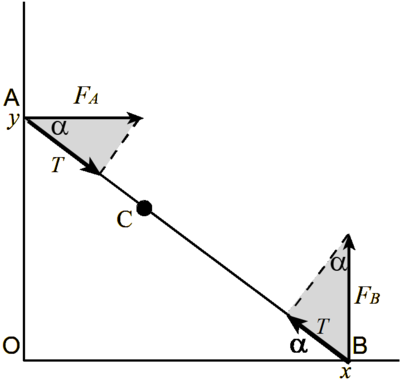
Let the rod be balanced, and the force pulling it together is equal to <math>T.</math> The grooves can create a force only along the normal, so they act on the rod with forces | Let the rod be balanced, and the force pulling it together is equal to <math>T.</math> The grooves can create a force only along the normal, so they act on the rod with forces | ||
<cmath>F_B = \frac {T}{\sin \alpha}, F_A = \frac {T}{\cos \alpha}.</cmath> | <cmath>F_B = \frac {T}{\sin \alpha}, F_A = \frac {T}{\cos \alpha}.</cmath> | ||
Revision as of 10:31, 22 February 2024
The segment of the shortest length
The segment ![]() has the ends on the sides of a right angle and contains a point
has the ends on the sides of a right angle and contains a point ![]() Find the shortest length of such a segment.
Find the shortest length of such a segment.
Solution
Let's imagine that ![]() is a spring rod that cannot bend, but tends to shorten its length.
is a spring rod that cannot bend, but tends to shorten its length.
The rod is fixed at point ![]() on a hinge without friction. The hinge allows the rod to rotate and slide.
on a hinge without friction. The hinge allows the rod to rotate and slide.
The ends of the rod can slide without friction along the grooves - the sides of the corner.
Let the rod be balanced, and the force pulling it together is equal to ![]() The grooves can create a force only along the normal, so they act on the rod with forces
The grooves can create a force only along the normal, so they act on the rod with forces
![]() For the rod to be balanced, it is required that the moments of the forces be equal relative to point
For the rod to be balanced, it is required that the moments of the forces be equal relative to point ![]() The moments of forces are:
The moments of forces are:
![]()
![]()
![]()